KNN
- 分类算法
- 监督学习
- 数据集是带Label的数据
- 没有明显的训练过程,基于Memory-based learning(基于记忆的学习)
- K值含义 : 对于一个样本X,要给它分类,首先从数据集中,在X附近找离它最近的K个数据点,将它划分为归属于类别最多的一类
K-means
- 聚类算法
- 非监督学习
- 数据集是无Label,杂乱无章的数据
- 有明显的训练过程
- K值含义: K是事先设定的数字,将数据集分为K个簇,需要依靠人的先验知识
不同点:
两种算法之间的根本区别是,K-means本质上是无监督学习,而KNN是监督学习;K-means是聚类算法,KNN是分类(或回归)算法。
K-means算法把一个数据集分割成簇,使得形成的簇是同构的,每个簇里的点相互靠近。该算法试图维持这些簇之间有足够的可分离性。由于无监督的性质,这些簇没有任何标签。
KNN算法尝试基于其k(可以是任何数目)个周围邻居来对未标记的观察进行分类。它也被称为懒惰学习法,因为它涉及最小的模型训练。因此,它不用训练数据对未看见的数据集进行泛化。
相似点:
算法都包含给定一个点,在数据集中查找离它最近的点的过程。
在KNN或K-means中,我们用欧氏距离来计算最近的邻居之间的距离,而不是曼哈顿距离。
原因是:
曼哈顿距离只计算水平和垂直距离,所以有维度的限制。欧氏距离可以用于任何空间距离的计算问题。由于数据点可能存在于任何空间,所以欧氏距离是更为可行的选择。
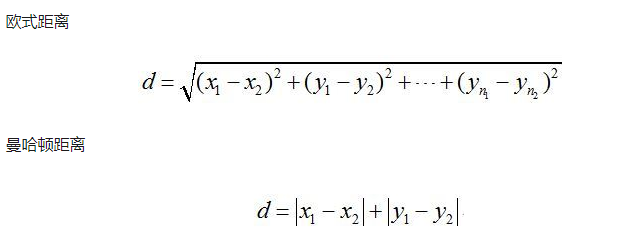
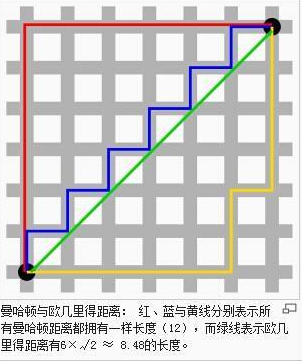
- 曼哈顿距离(Manhattan Distance)就像曼哈顿的街道一样,只有水平和垂直的线段。
- 欧氏距离(Euclidean Distance)则是可以量测任意方向的线段。
参考资料:
https://zhuanlan.zhihu.com/p/31580379
https://www.cs.cmu.edu/~schneide/tut5/node9.html
版权属于:soarli
本文链接:https://blog.soarli.top/archives/192.html
转载时须注明出处及本声明。

