走进数据科学:博大精深,美不胜收
整装待发



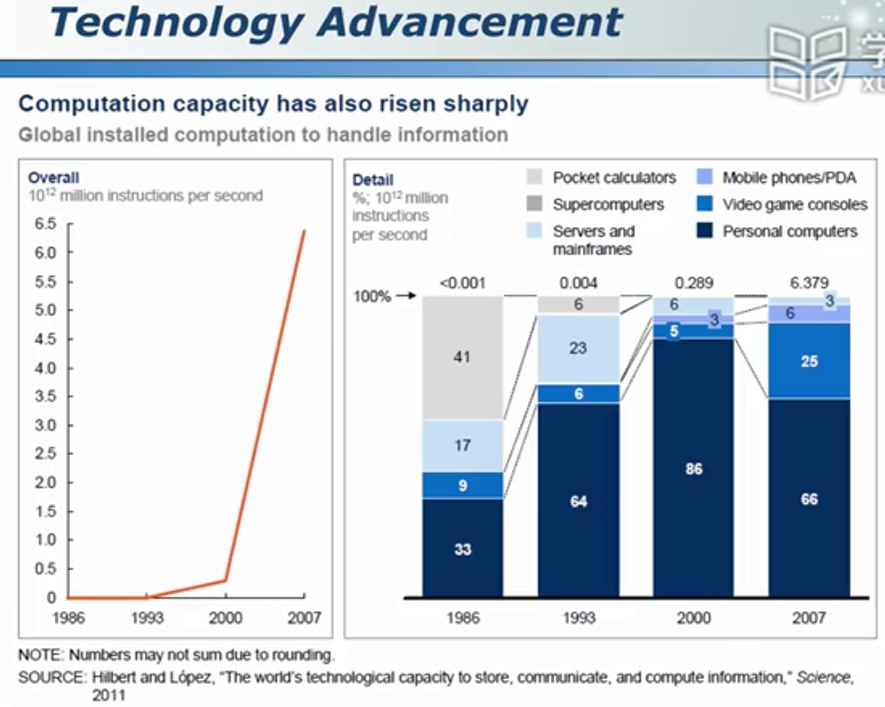
学而不思则罔
相关书籍




多学科交叉




知行合一

大数据


数据挖掘的应用
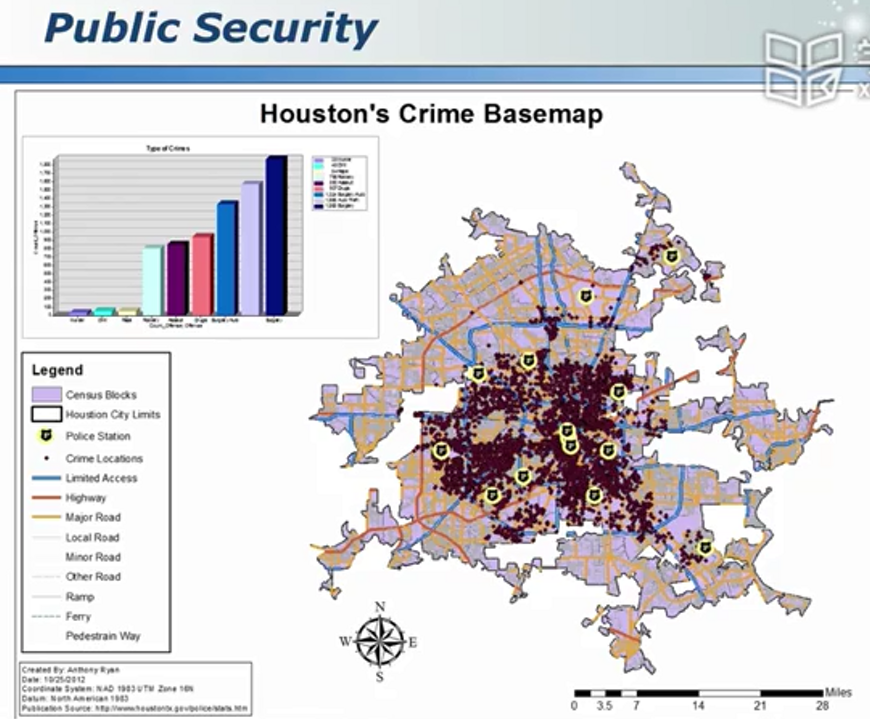





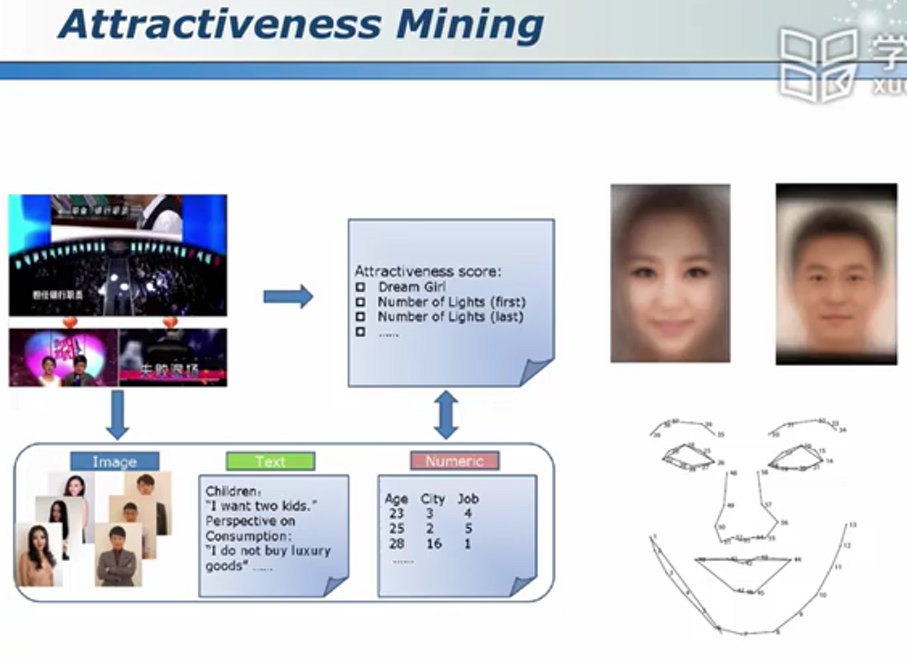
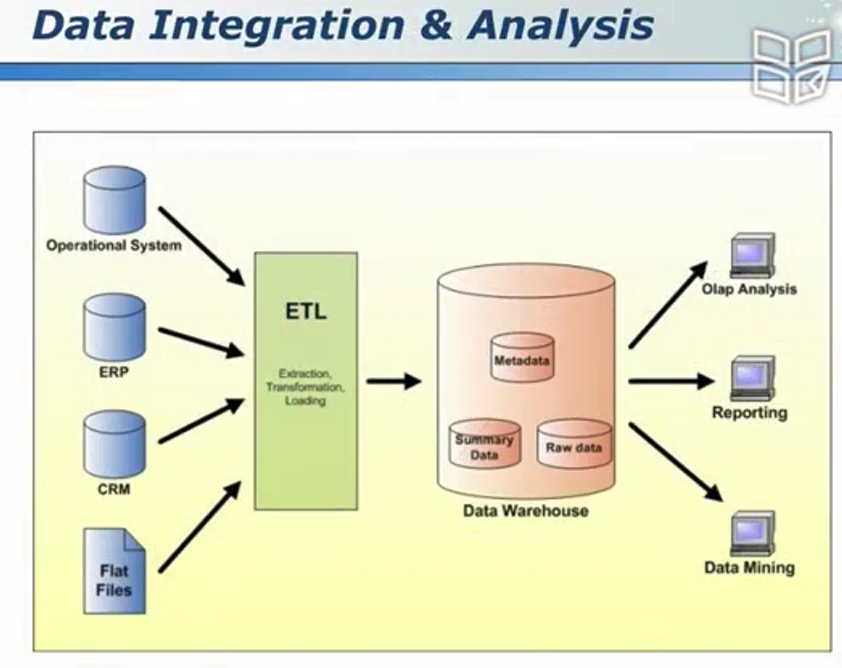
从数据到知识
数据孤岛 - 公开数据

数据挖掘





知名商务企业级软件

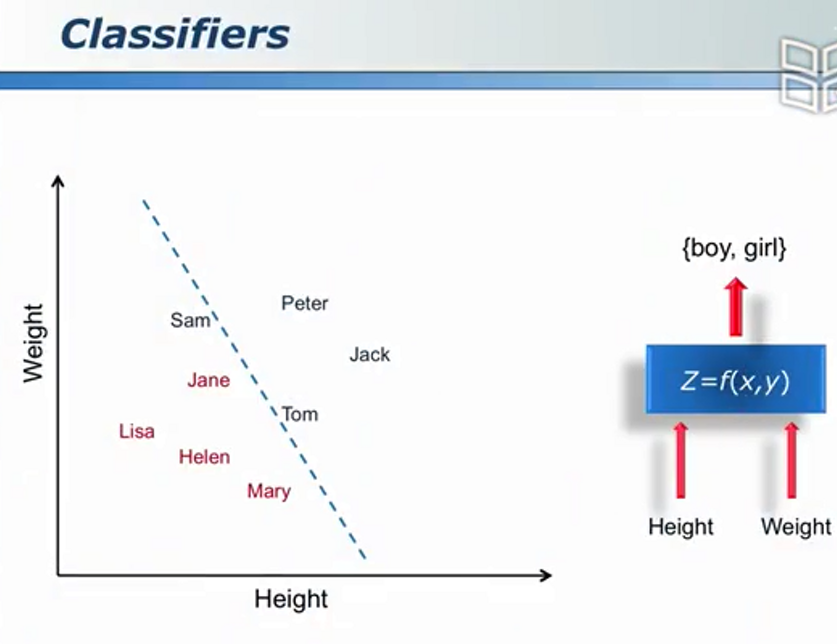
分类问题
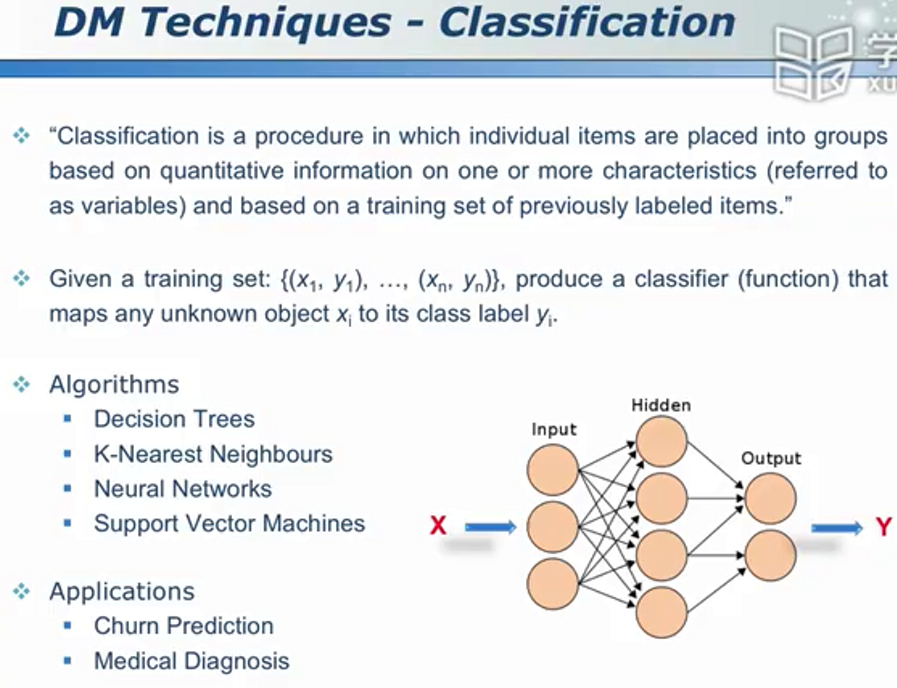
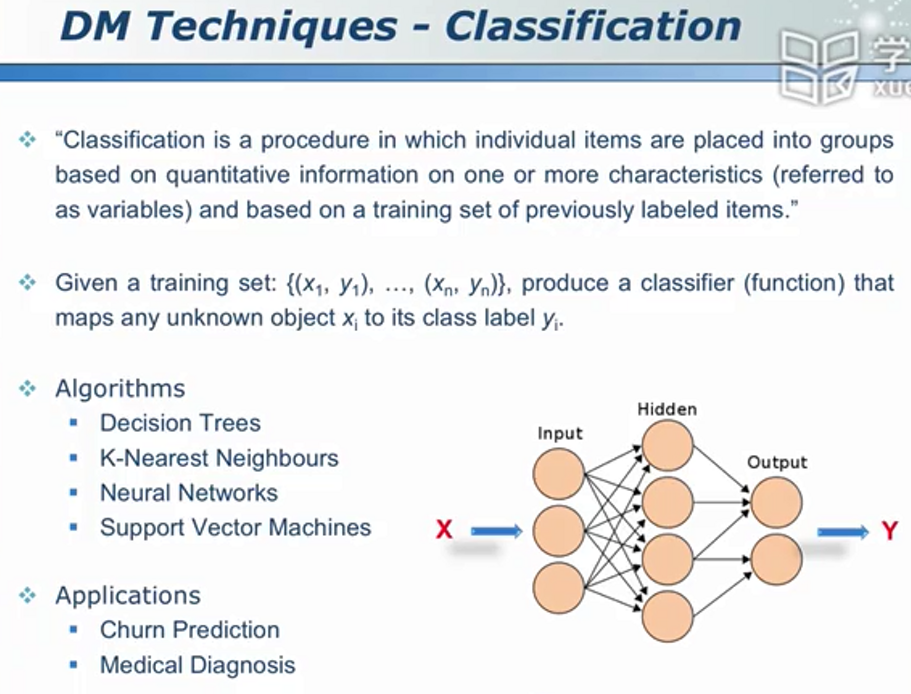
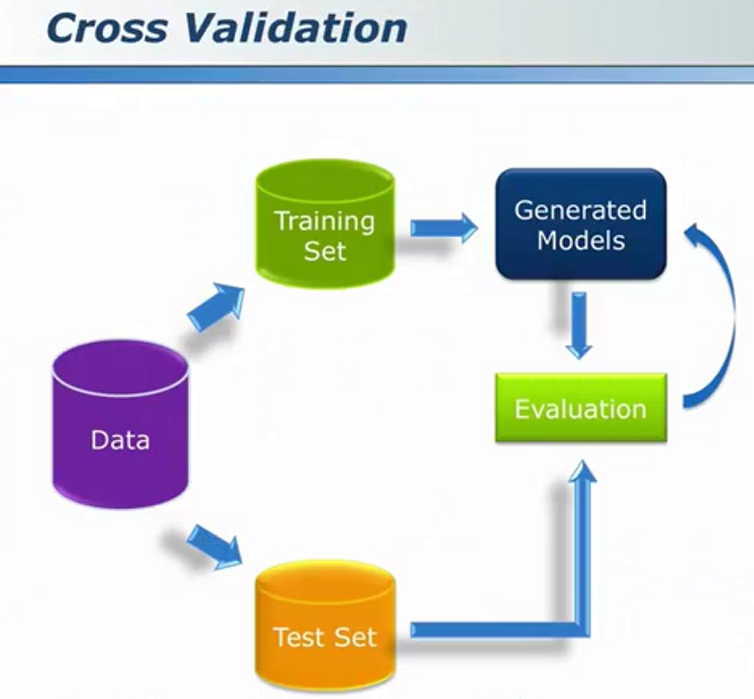
训练-->得到模型-->预测
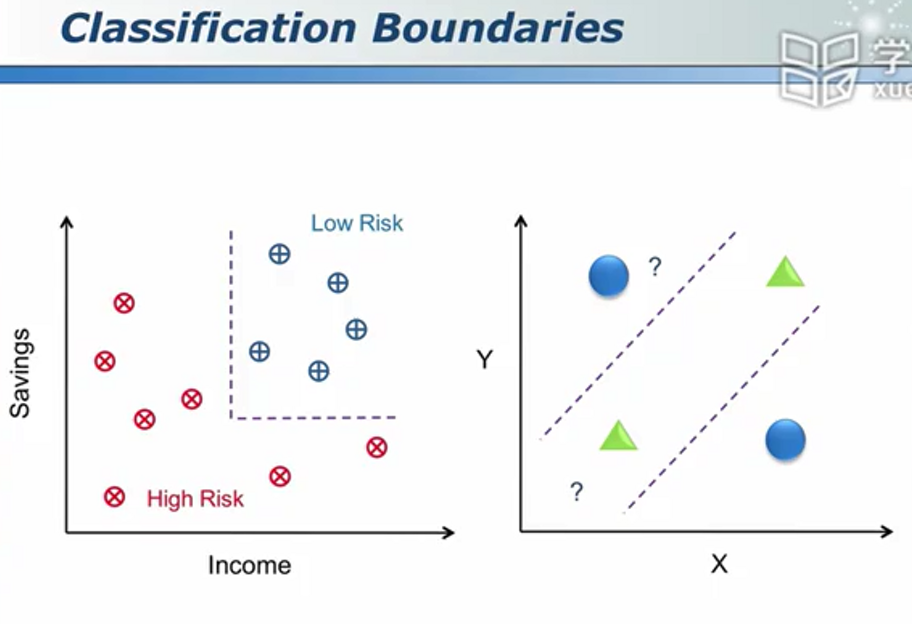
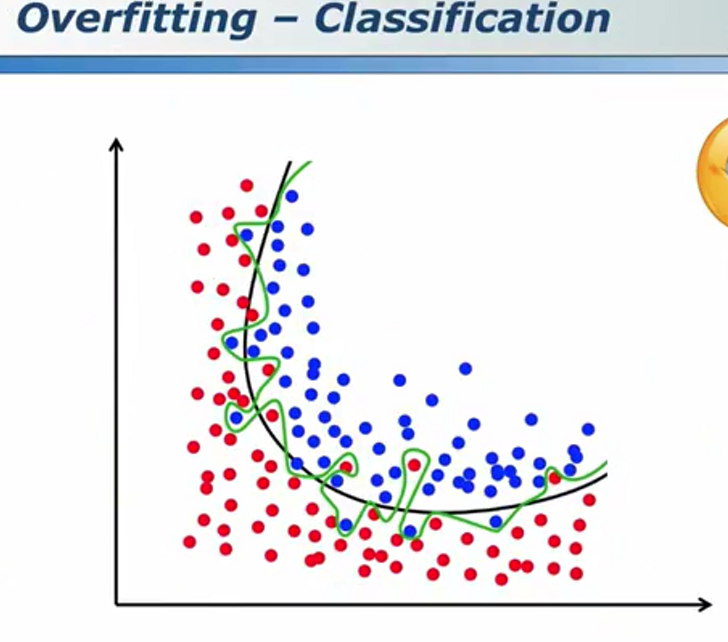
相对于绿色的那条分类器,我们普遍认为更加平滑的黑色的那条分类器更加可靠。
混淆矩阵
男人与女人问题(用以检验预测准确率)

ROC曲线
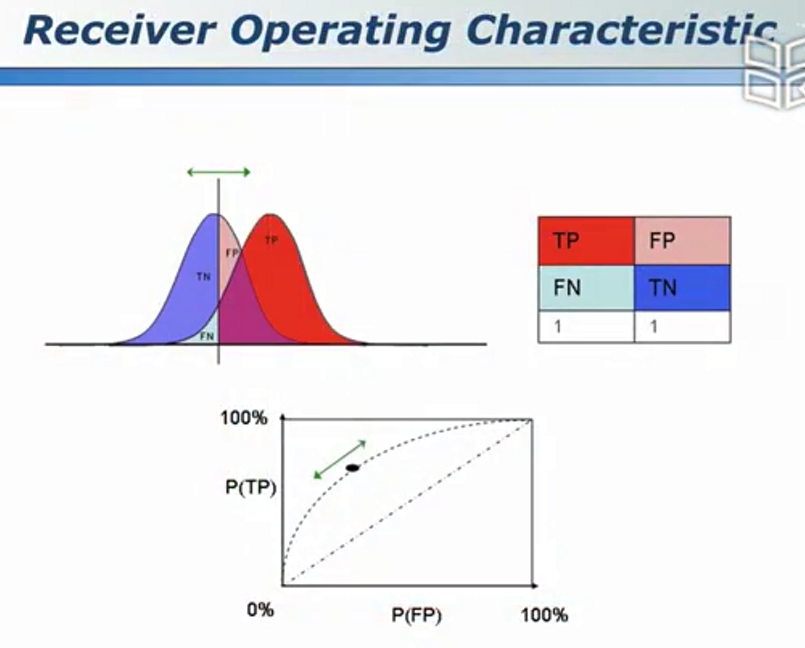
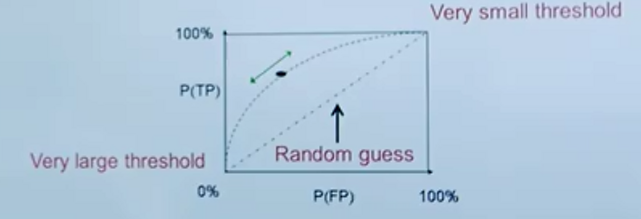
random guess代表50%;
AOC是预测准确率,属于0~1区间,越接近1则模型越好。
代价成本 - 同样是误判,危害一样大吗?
误杀罪犯?误放罪犯?;误把正常邮件进垃圾箱?误把垃圾邮件视为正常?;误诊:白视为黑?黑视为白?

因此误差是要讲究权重的。
模型效益的评估 - 用模型与不用模型的差别
把可能卖商品的人集中放置,在预算不够时只需联系权重排名靠前的人。
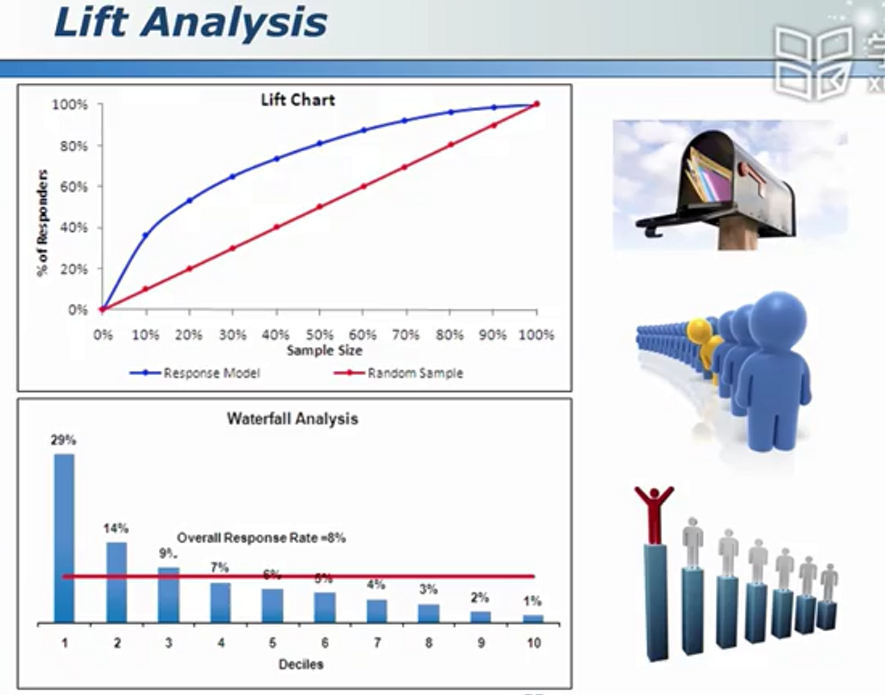
聚类及其它数据挖掘问题
聚类无事先的、人为的标签
聚类属于无监督学习
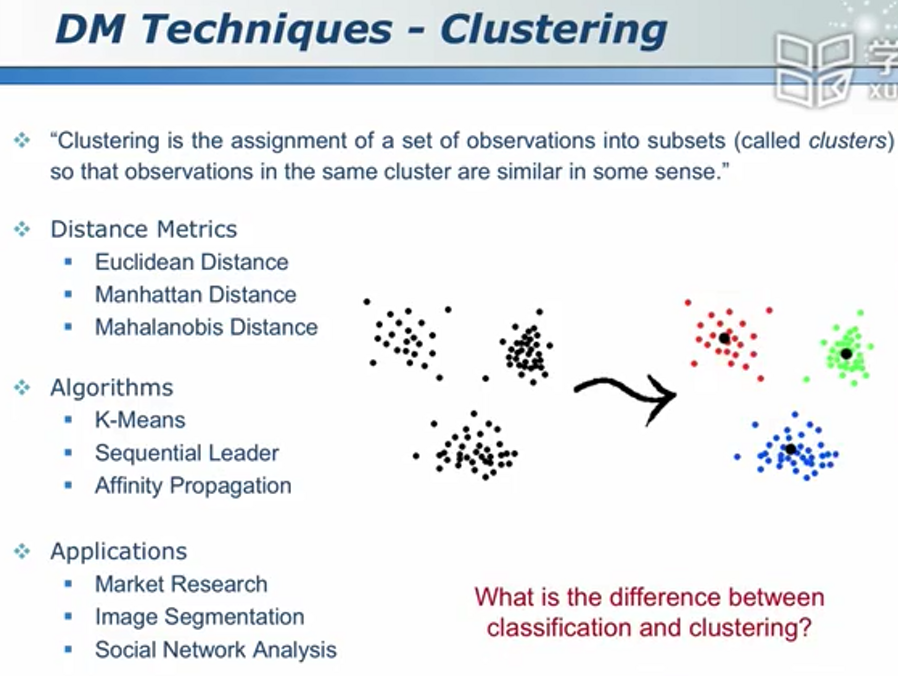
普通聚类和层次性聚类
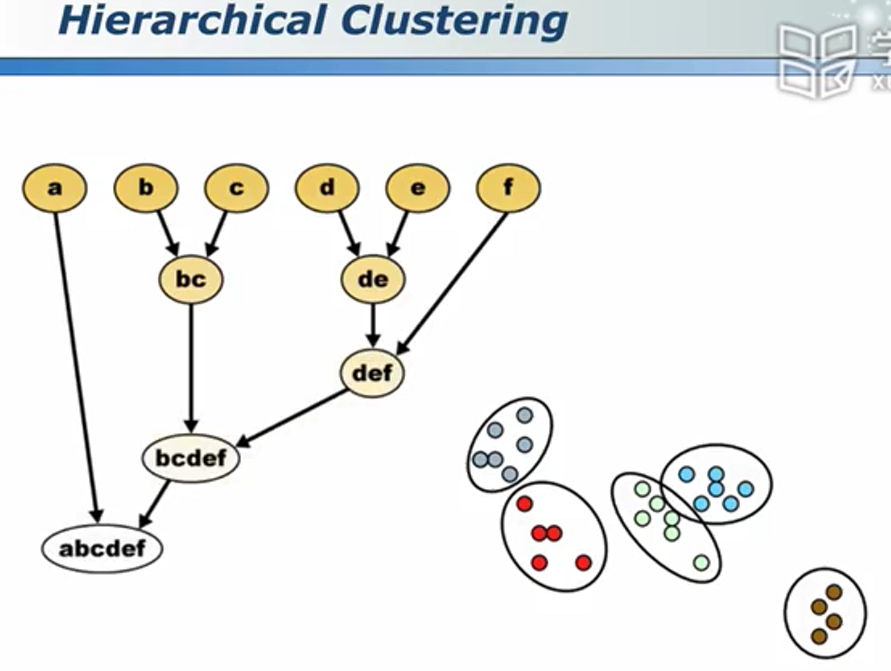
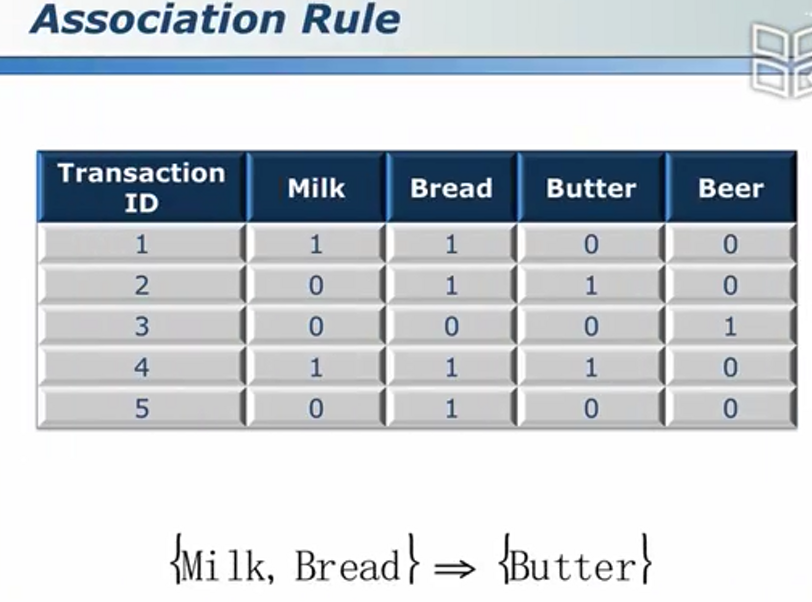
关联规则

线性回归
线性回归未必一定会拟合出直线,也可能拟合出曲线。(线性指的是参数和变量之间是线性的)

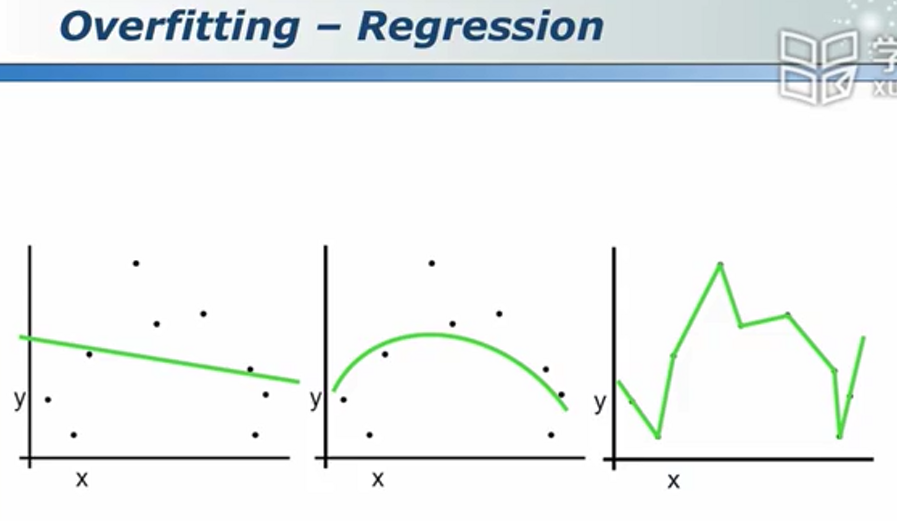
上图中,我们认为第二类回归相对较好(既不是“啥都不知道、又不是“死记硬背”)
数据可视化 - 增强“可解释性”
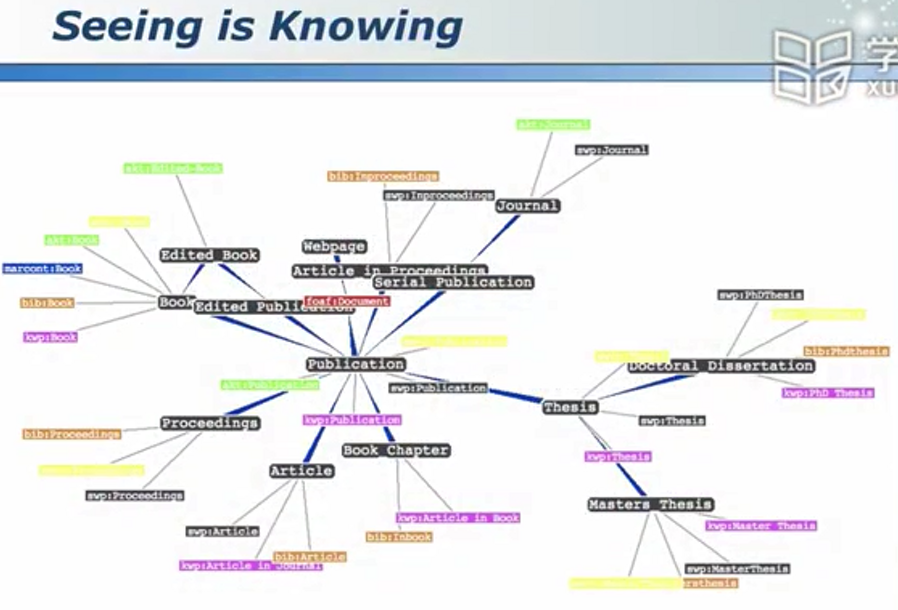
仪表盘是个好主意:

数据预处理 - 数据挖掘中的重难点


隐私保护与并行计算
互联网与隐私


隐私保护的数据挖掘

巧妙设计问题使得被调查者可以放心回答,调查者可以得到准确信息

云计算 - 实现较高的资源利用率

“虚拟化”的既可能是服务器资源,又可能是软件/服务,如Photoshop、Matlab等。
串行/并行计算

使用GPU进行计算

工作站

开发板


数据挖掘=数据+模型/公式/算法+算力
没有免费的午餐

迷雾重重
纳斯达克股市

量化交易:用于克服人性贪婪的弱点
没有规律的数据不能“挖掘”

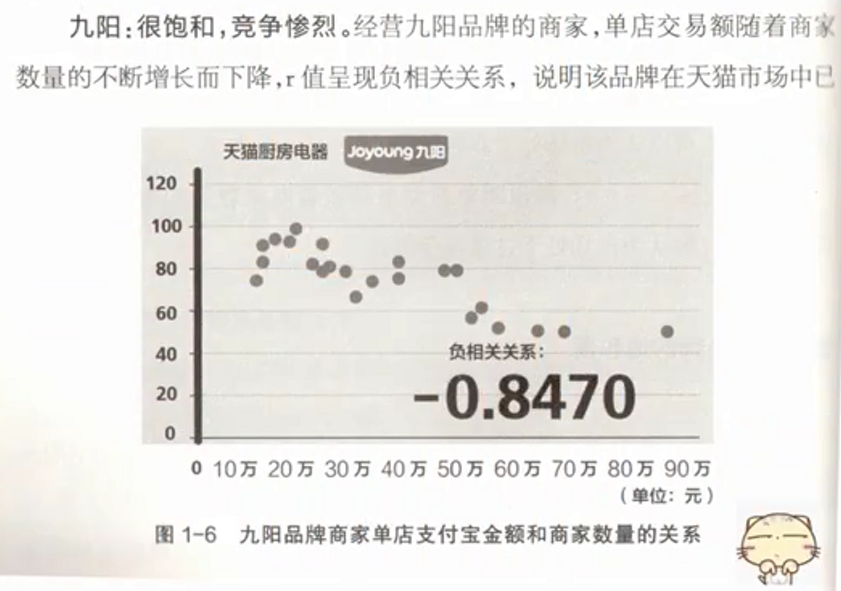
预测实例
看似负相关
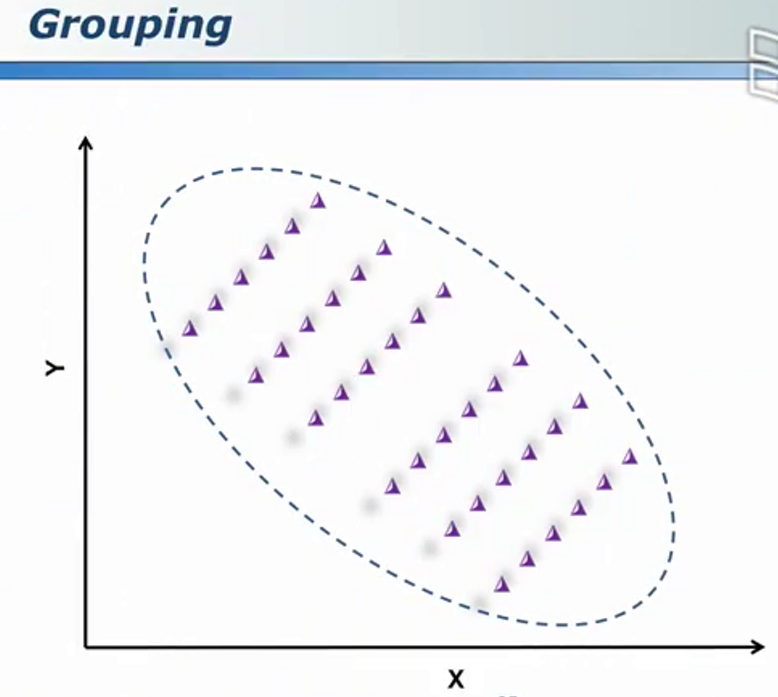
内部则出现正相关
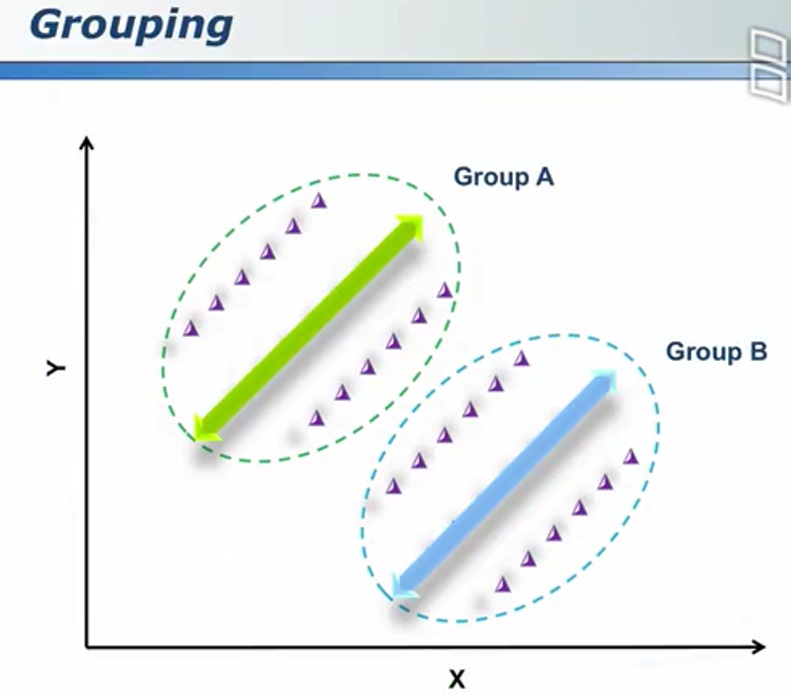
分类方法可能是人群种类
例如:暴力游戏一定会增加社会犯罪率吗
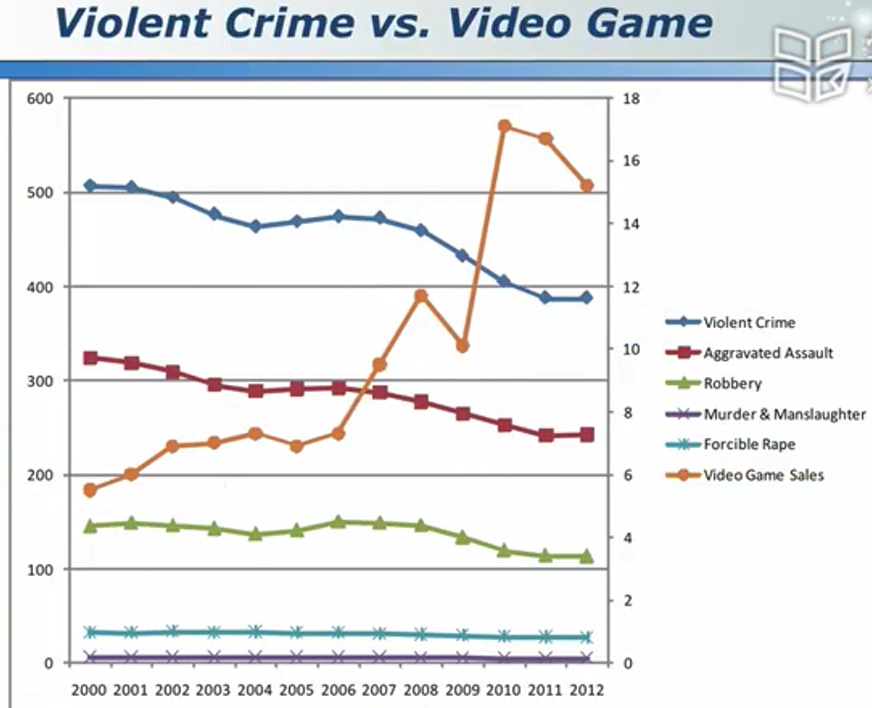
只有两条线,未必能够得到准确的结论。
身高和事业成功一定有关吗


样本本身的偏差
例如:


真的应该在弹着点分布密集的地方加固吗?
思考:
这些提供数据的飞机都是幸存的、能飞回来的飞机!
换句话说,或许能够提供真正需要加固的位置的飞机多半都死在路上了,无法提供参考数据。
思考2:
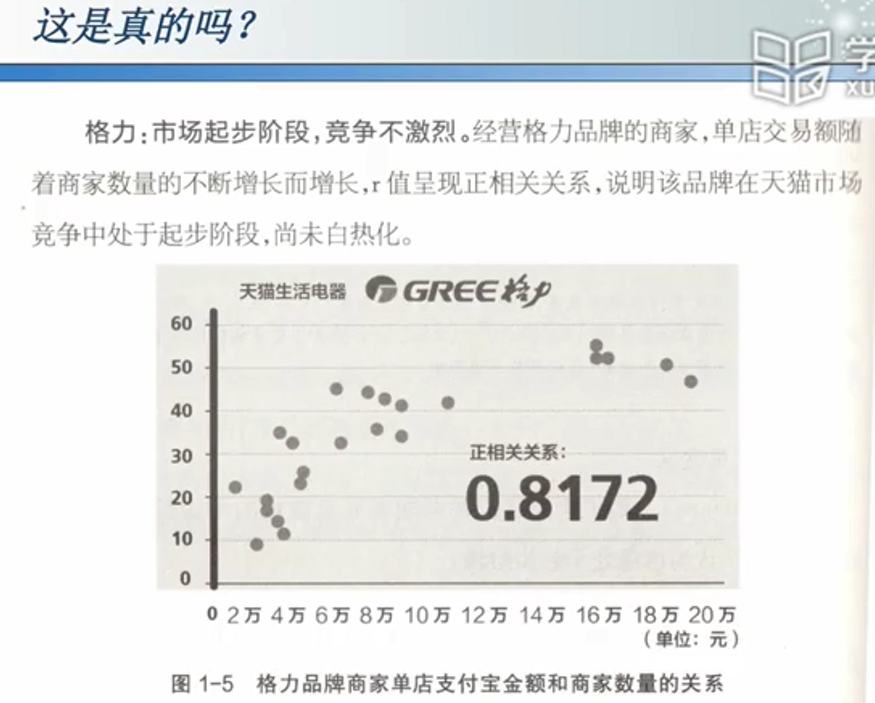
正着看和倒着看会出现截然相反的结果!
首要原因:
时间维度的缺失!
思考3:
首要原因:
同样是时间维度的缺失!
视角导致偏差的小测试


结论:
数据分析用的好:找出了数据背后隐藏的规律;用的不好:可能会犯下非常荒谬的错误!
数据预处理:抽丝剥茧,去伪存真
数据清洗



数据缺失、错误数据、不适用的数据

如何处理缺失的数据
忽略、猜测、重新收集、填写0、填写均值

为使模拟的数据更加可靠,可以类似于高斯分布进行采样,下图可联想男女的身高体重分布
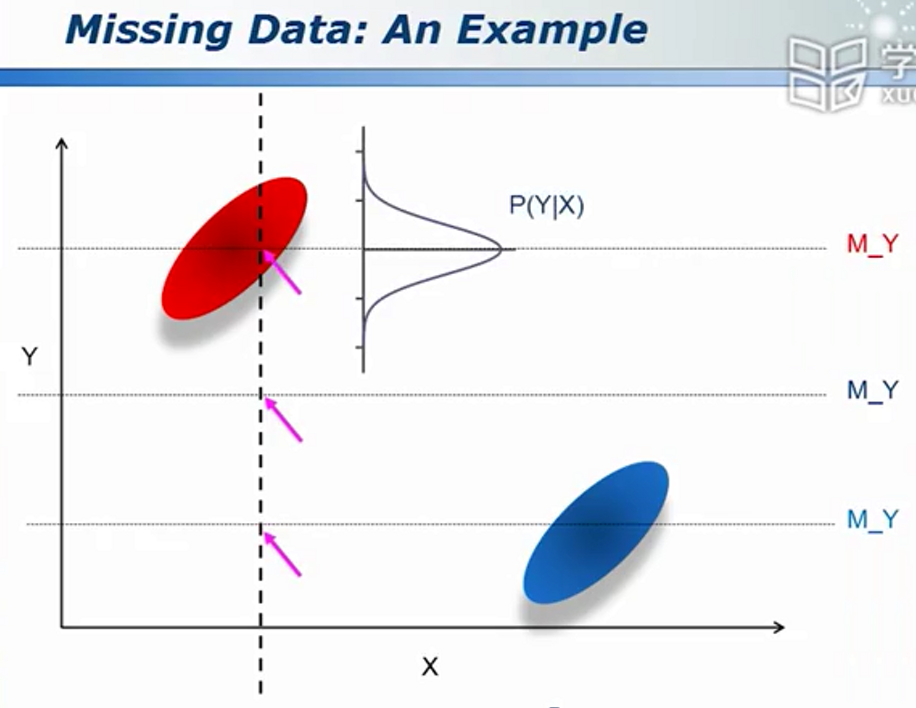
离群点的处理
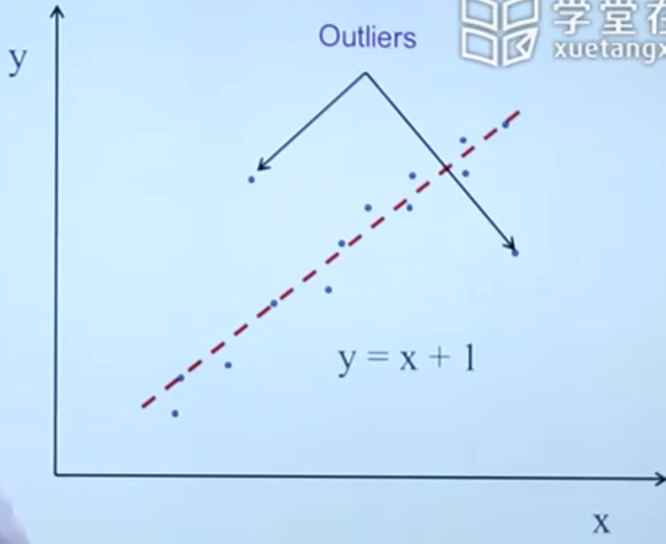

异常点
和离群点的区分:
如姚明的身高,为离群点。一个得巨人症的人数据:异常点。
异常值与重复数据检测
离群点的检测
离群是一个相对的概念,若下图所示的欧氏距离是一个可行的方法(方法不唯一)

相应的,值越大,说明其为离群点的可能性越大,对应下图的圆形面积越大。

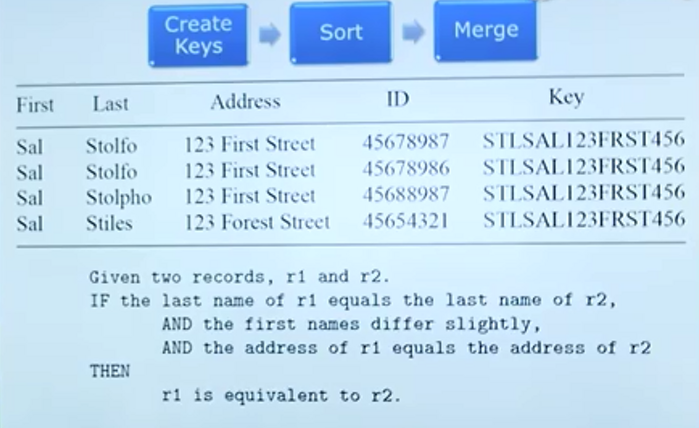
怎样从海量数据中找出相同的目标
在物流中,写不同的名字,不同的电话,甚至写不写某某区可能都能被寄到同一个人手中。我们怎样从数据中挖掘出表面上不同,实则相同的信息?
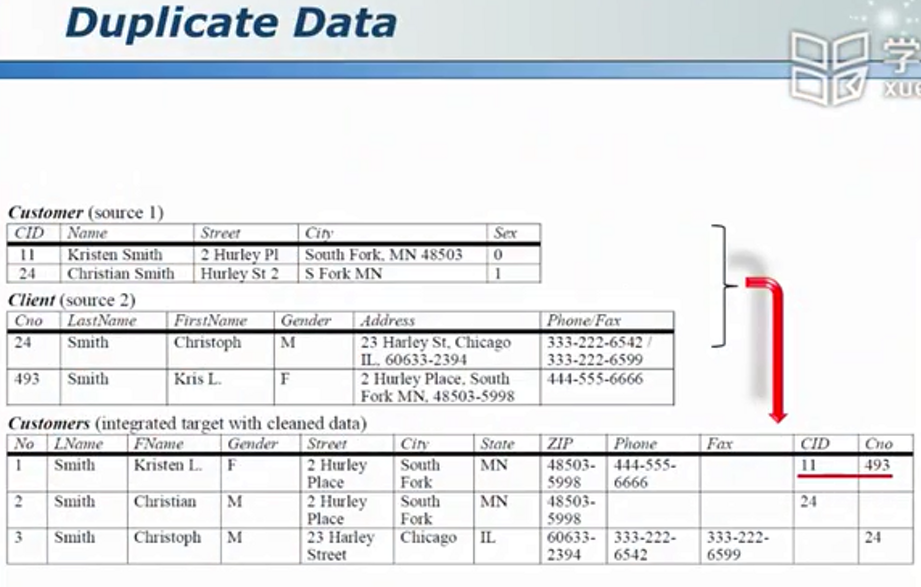
对比数据
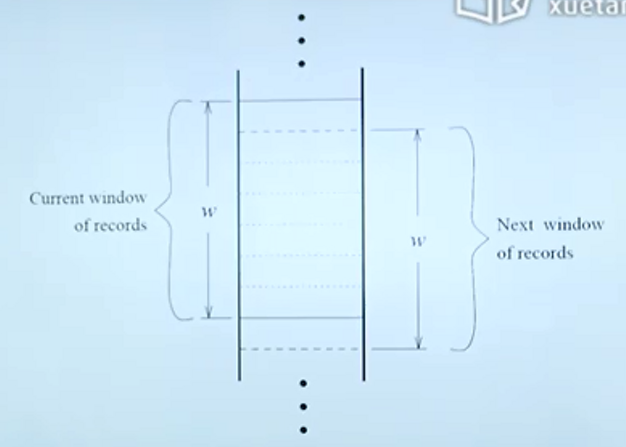
假设有100W条数据,如果每增加一条数据就两两比较显然不现实。因此可采用“滑动窗口”技术。使得每一条数据与特征最接近的100(可设定)条数据进行比较。
当然,前提条件是高度疑似的数据在数据库中是挨着的。
类型转换与采样
数据类型转换


对于RGB,我们该如何编码
化为“0,1,2”?那么默认则认为0,1对应的颜色接近,0,2对应颜色距离较远。显然未必合理!
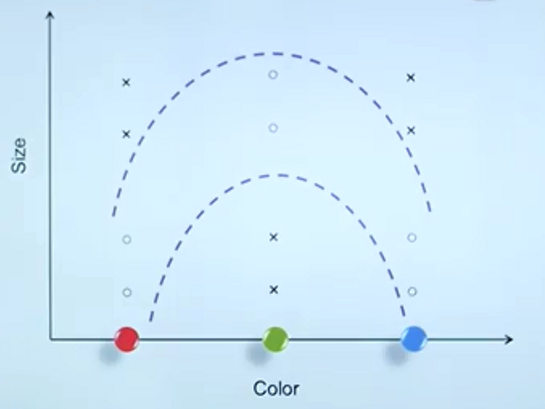

编码的不同会导致问题结构上的不同(或数据在空间中的分布不同),进而可能使得一个较难的问题变得简单或适得其反!
很多软件包通过增加维度来优化处理:
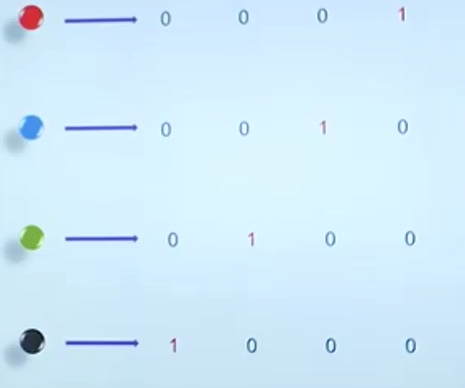
采样
I/O负担大-->考虑进行数据采样进而降低时间复杂度

不平衡数据
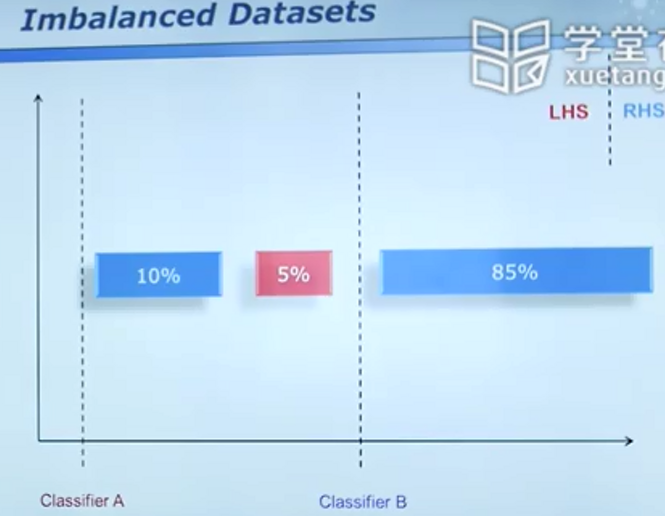
对于上图,很多算法最终会收敛到A分类器,因为A的误判率相对较低,然而事实上B更加合理。
(联想医生因为某种疾病致病率仅有1%便对每个病人因99%的正常率贴上无病的标签会造成更大的损失)
相应更合理的算法:

向上采样
用合理的方法随机生成点

找出并合理利用边缘点
很多时候,边缘点往往更有价值,5%的点能够实现95%的价值,我们要试图找出它们
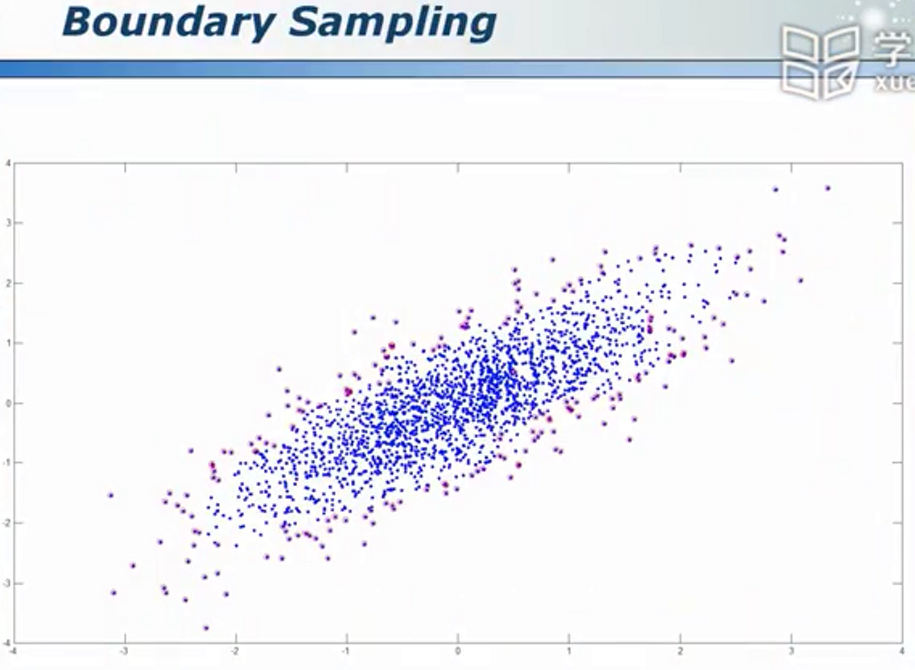
数据描述与可视化
数据标准化

数据描述(均值,中位数等)

数据的相关性

没有线性相关性和不相关是两个不同的概念
数据可视化 - 百闻不如一见

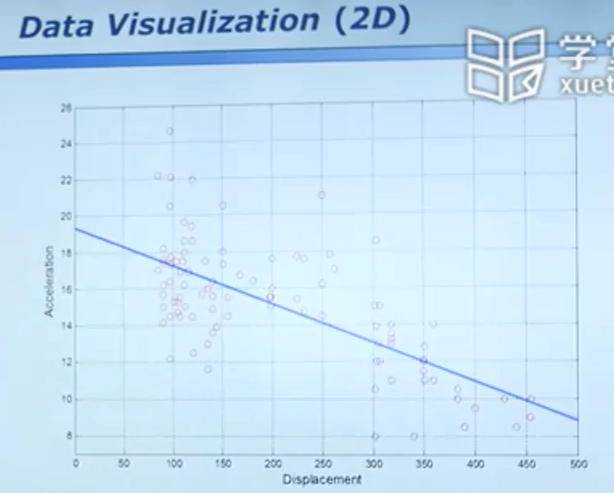
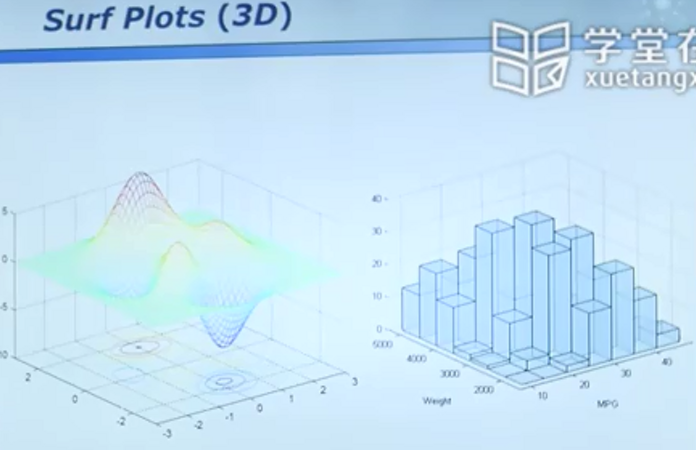
四维数据的展示
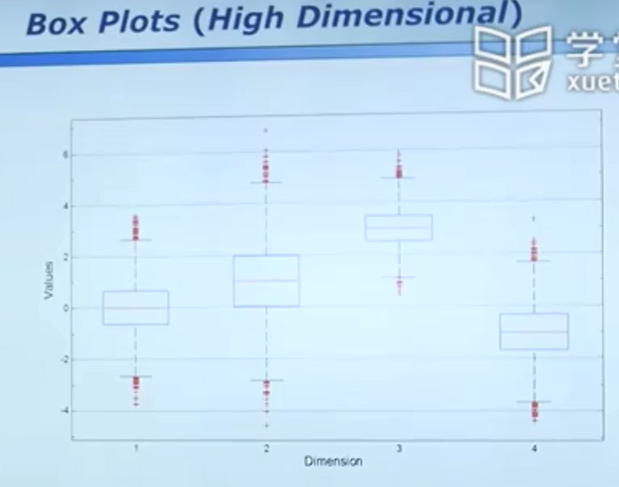
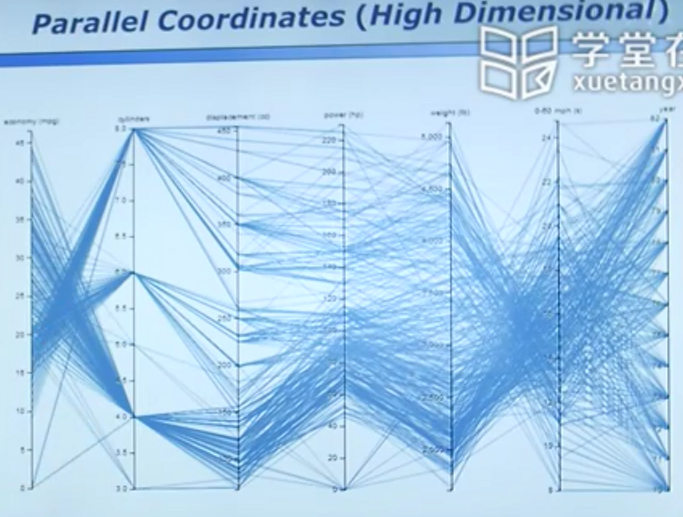
高维数据

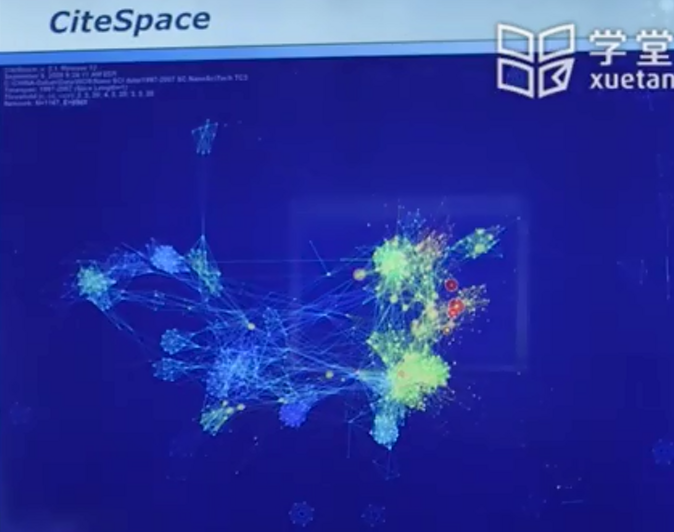
可视化工具

特征选择
相关属性的选择

属性的划分
下图可联想男人女人的身高:
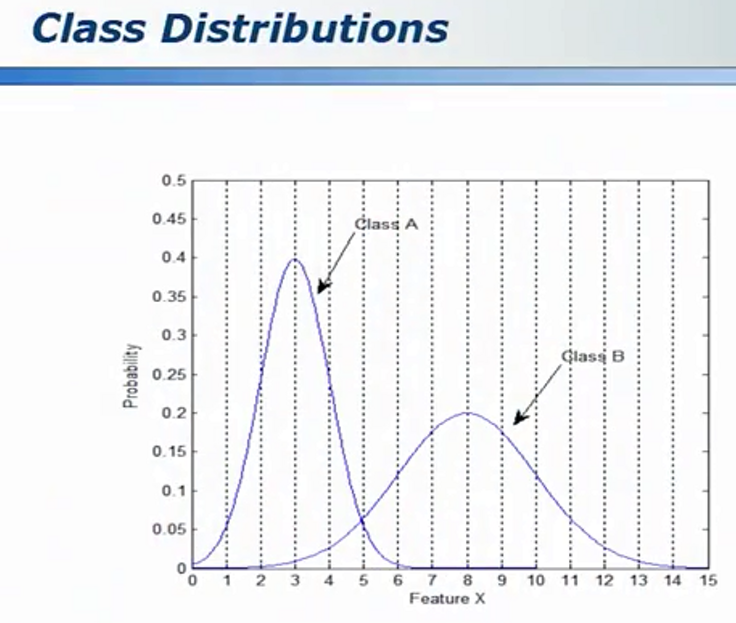
“刚才见了一个人,你猜是男人还是女人?” -50%男,50%女
“刚才见了一个在抽烟的人,你猜是男人还是女人?”-%95男,5%女
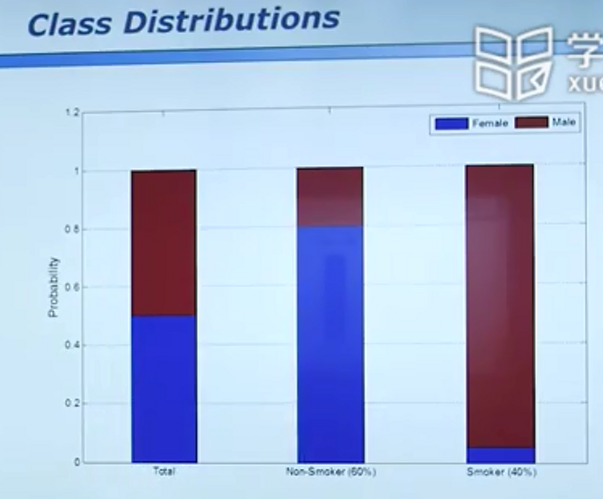
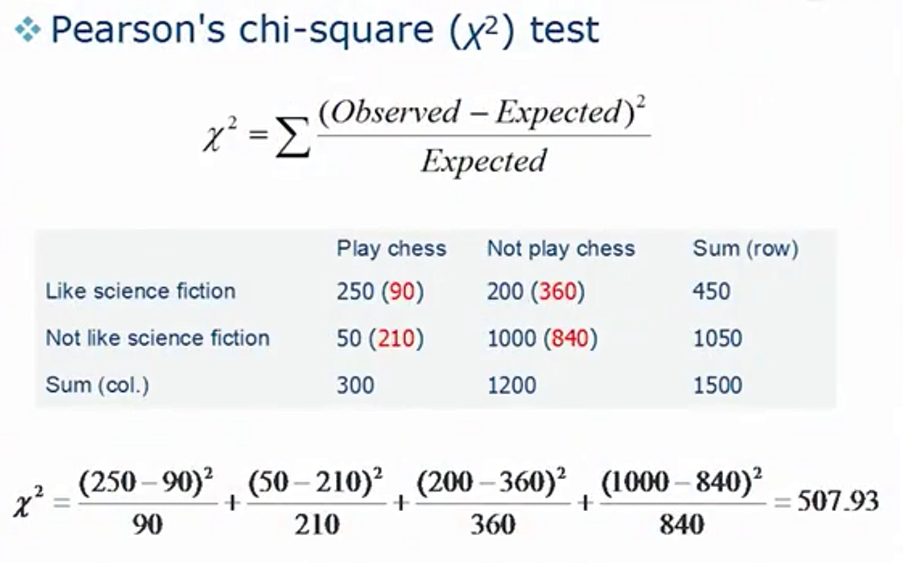
熵 - 属性相关性的定量描述
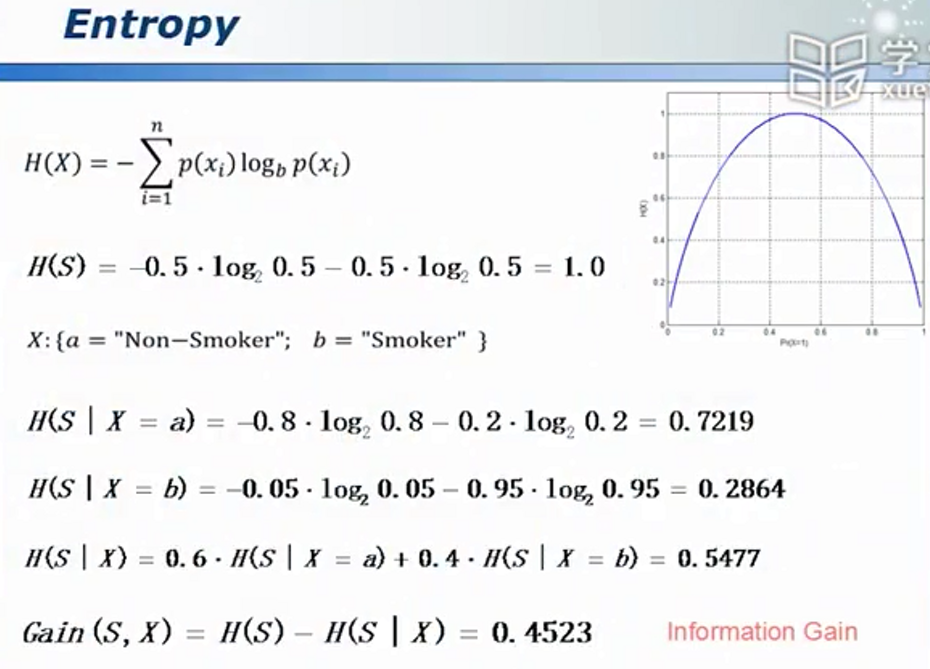
其中, (信息增益)越大越好,其代表得到一个新的属性后原问题不确定性的减少量。
(信息增益)越大越好,其代表得到一个新的属性后原问题不确定性的减少量。
优化算法 - 不去搜索不必要搜索的内容
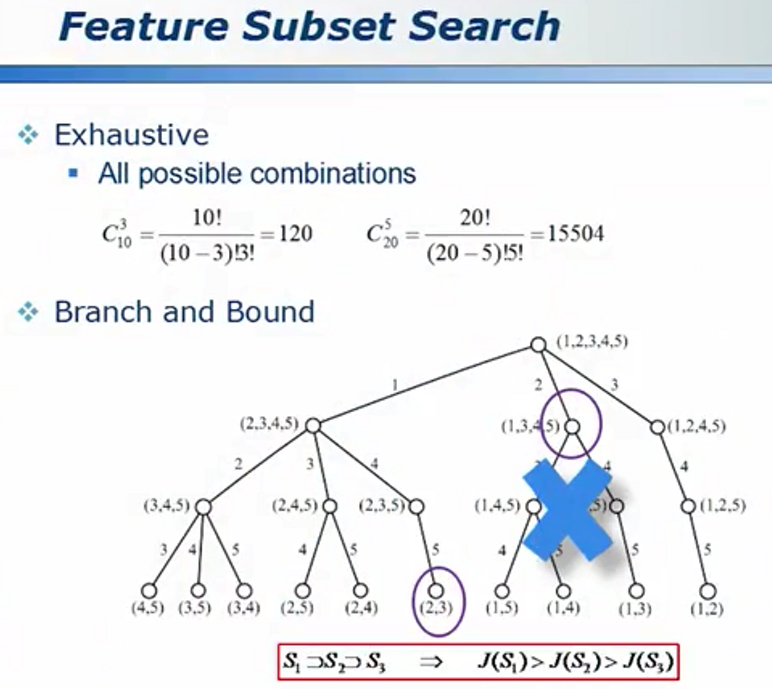
属性组合的优化


选择合理的算法(如模拟退火)
主成分分析
特征提取(不同于特征选择)
(哪里不同?为什么不同?)

不是简单地挑选像素,而是做了差分、线性组合等进而筛选提取出了边缘像素。
主成分分析
同样是从三维映射到了二维,不同的映射方法得出的结论差别很大。


一个简单的例子(通过坐标轴的旋转方便数据特征的提取)

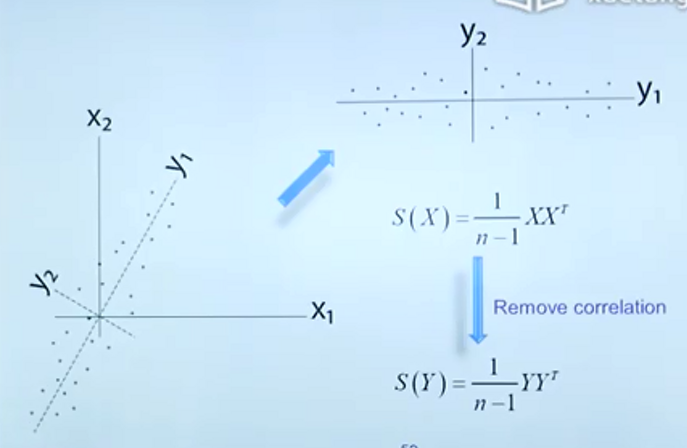

转化为优化问题

拉格朗日乘数法 - 带条件的约束法

转化为矩阵的分解问题

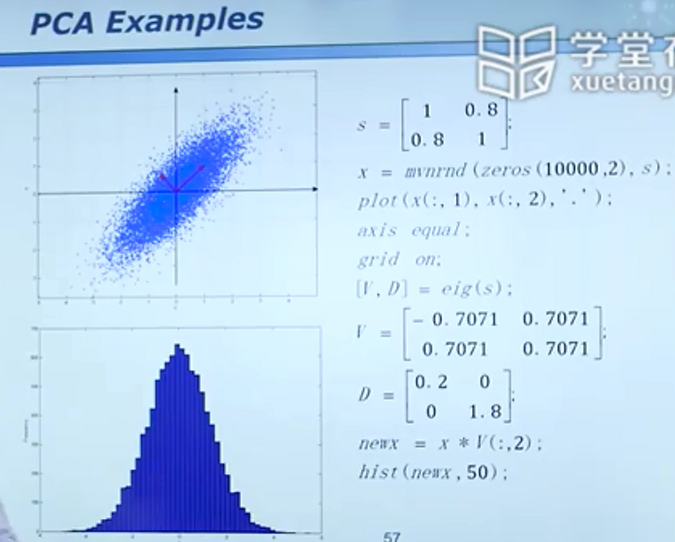

但是对于不同种鱼,相同的模型不再适用

线性判别分析
PCA(主成分分析)- 无监督学习
https://www.cnblogs.com/fuleying/p/4458439.html
主成分分析无标签,因此若要做分类问题,PCA得到的数据显然无法进一步处理(原本可以分开的数据经过投影无法分开)。

线性判别分析
经过投影,可以方便地分开数据,如下图中右侧的坐标面所示。

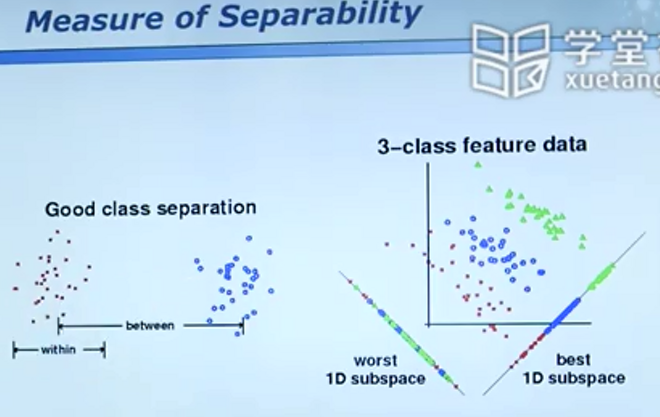
在下图中,看似往x1轴投影,二者距离较远,实则混在一起的点更多。故相对x1应选取x2轴。
然而如图2,旋转一个角度再去投影则可以得到更好的结果。
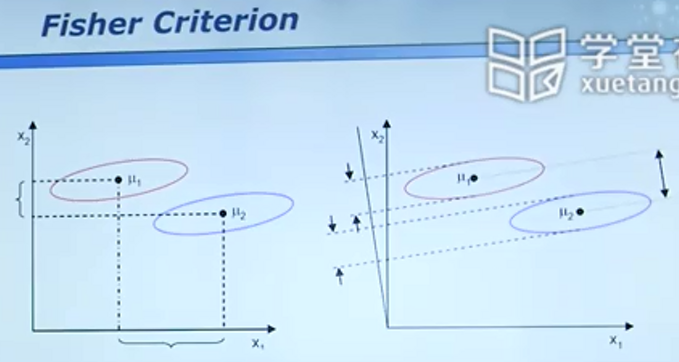
投影标准的检验:

不同投影方案,得到的J值越大越好。


针对两分类问题,可以采用这种算法得到所需投影方向

举个例子



结论
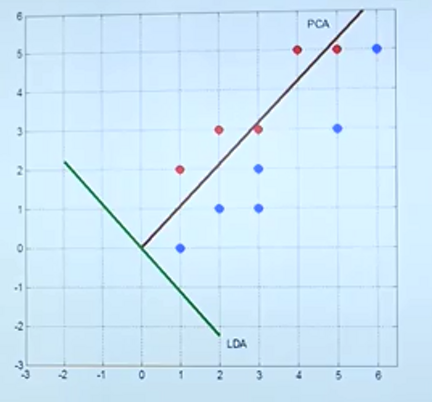
多分类问题

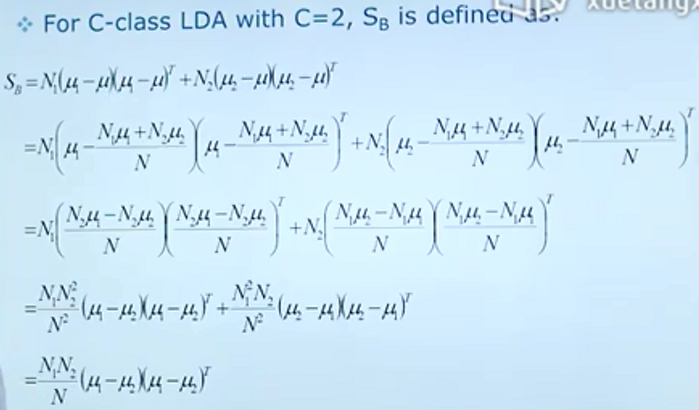
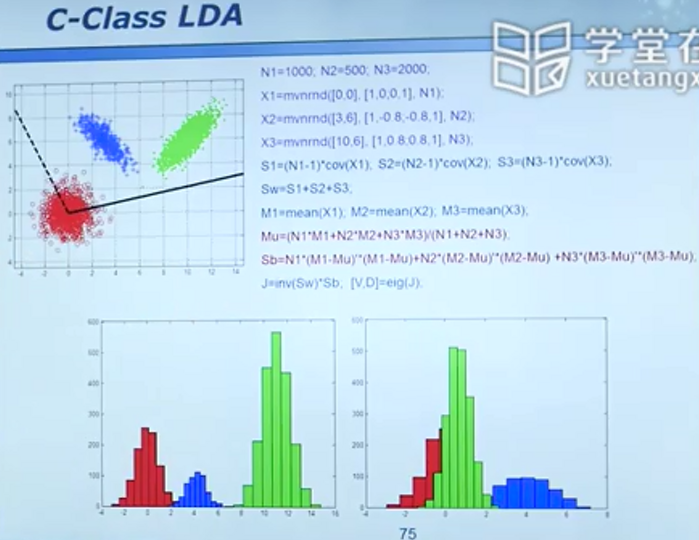
一个三分类的Matlab实现
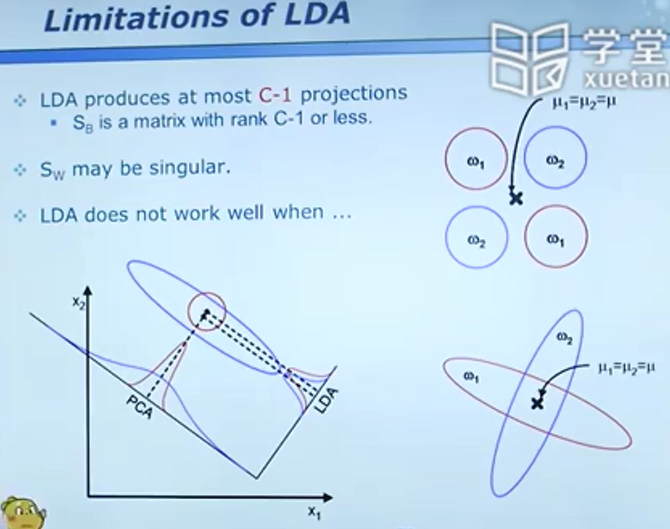
当维度大于样本数时,sw会变成奇异矩阵,这时可先使用PCA等方法进行降维再去处理
推荐资料:

从贝叶斯到决策树:意料之外,情理之中
贝叶斯奇幻之旅

分类属于监督学习

分类问题实例
训练/学习

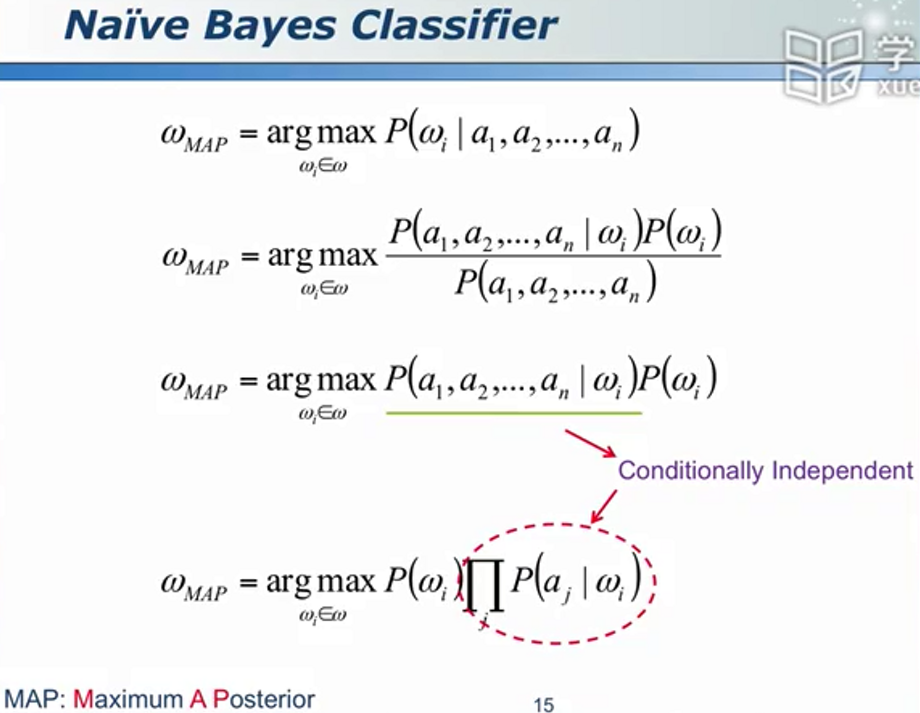
贝叶斯定理



B命中的概率还需要用该公式计算(因为二者可能同时命中)




朴素是一种美德
条件独立 - 朴素贝叶斯

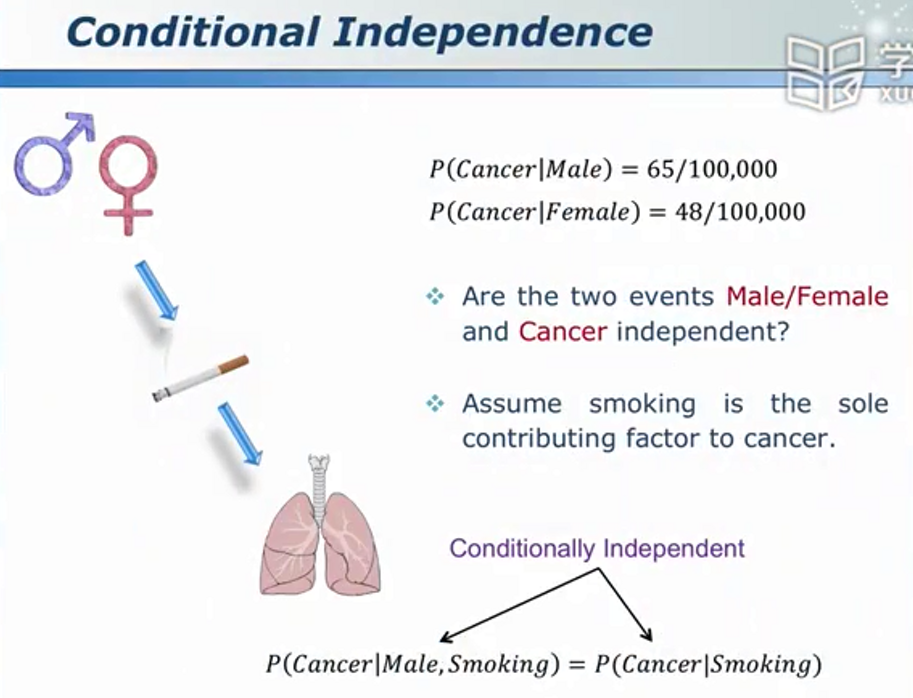
条件独立的应用实例 - 肺癌与性别有关吗?


其中,
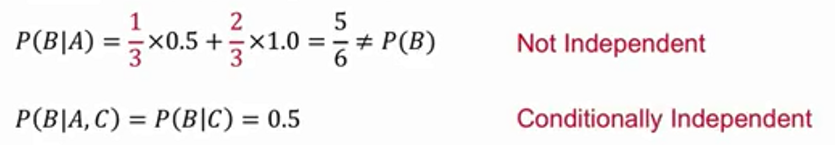
独立和不相关
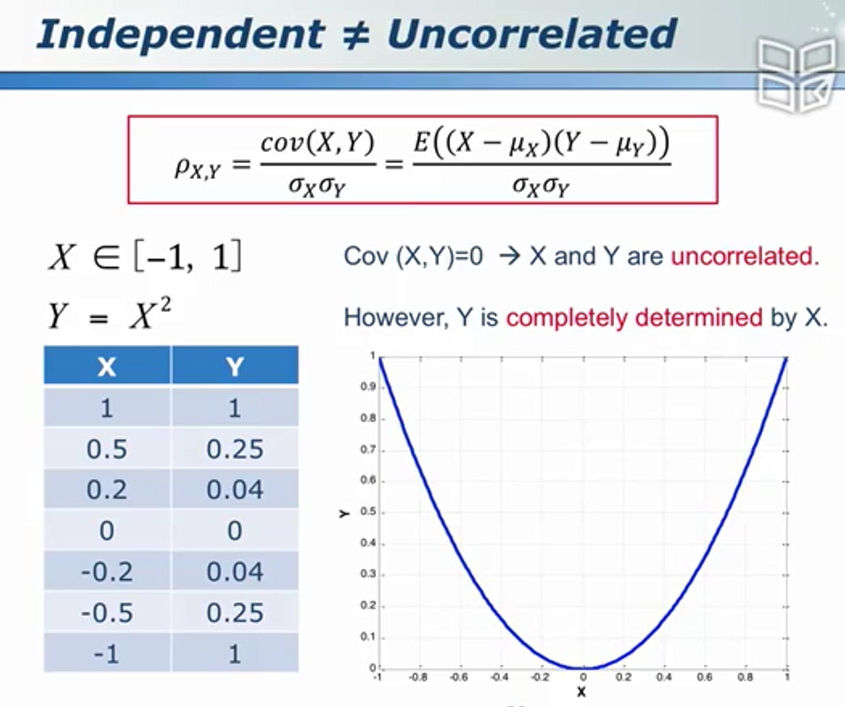
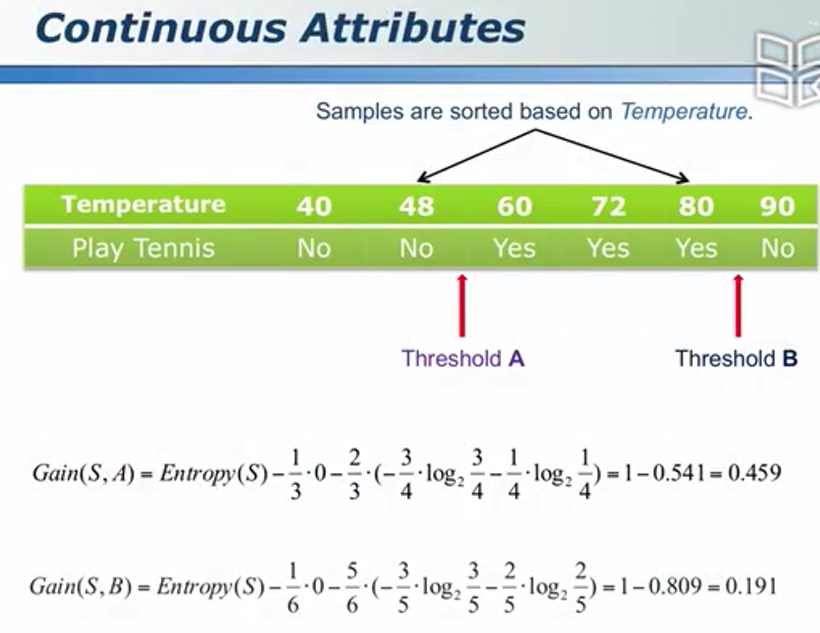
离散和连续

数据集示例 - 是否打球
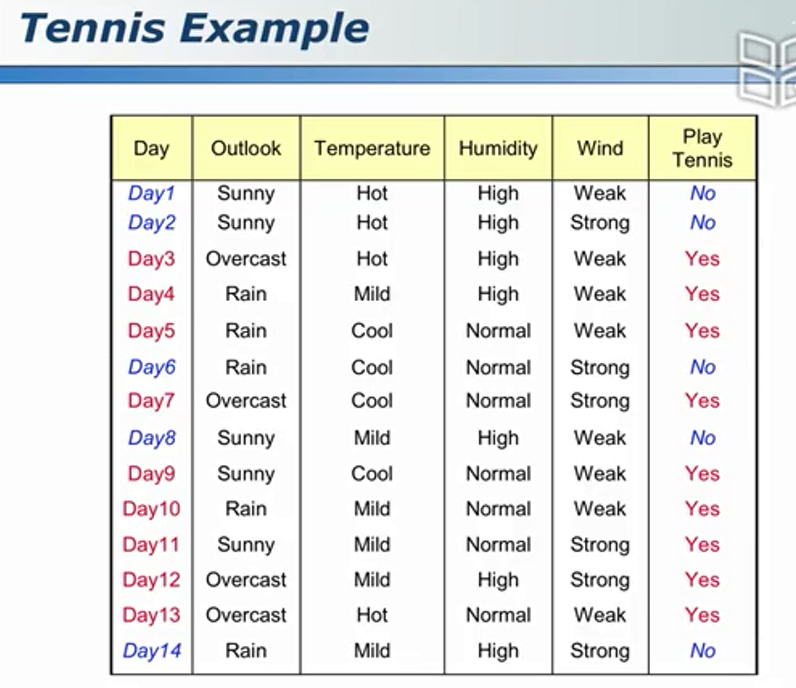

文本分类示例




数据、规则与树
决策树 - 一种符合人脑逻辑的分类器

对客户模型建模



对于同一个数据集,可以生成的树未必唯一
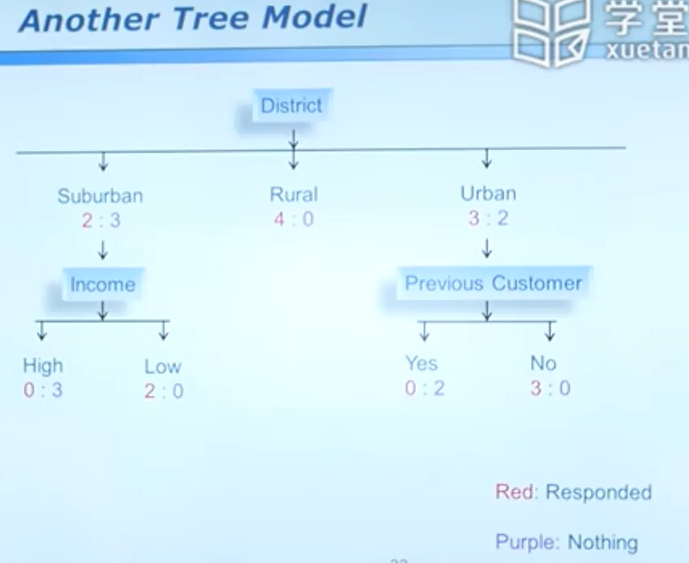
概述:

一般规律:
要用尽可能简单的方法对事物进行分类。
植树造林学问大 - 决策树的建立
- 把比较强大的属性放在上面

信息增益 - 得知一个信息后对解决问题的帮助


算法逻辑

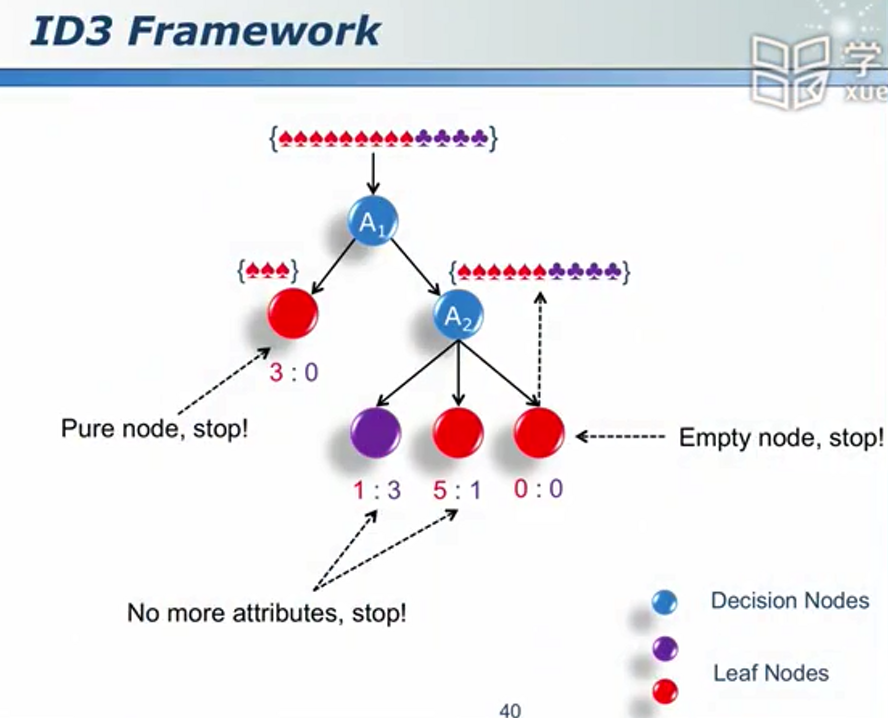
过学习 - 训练集:你比我好;测试集:我比你好

过学习的解决方案:剪枝 - 合并
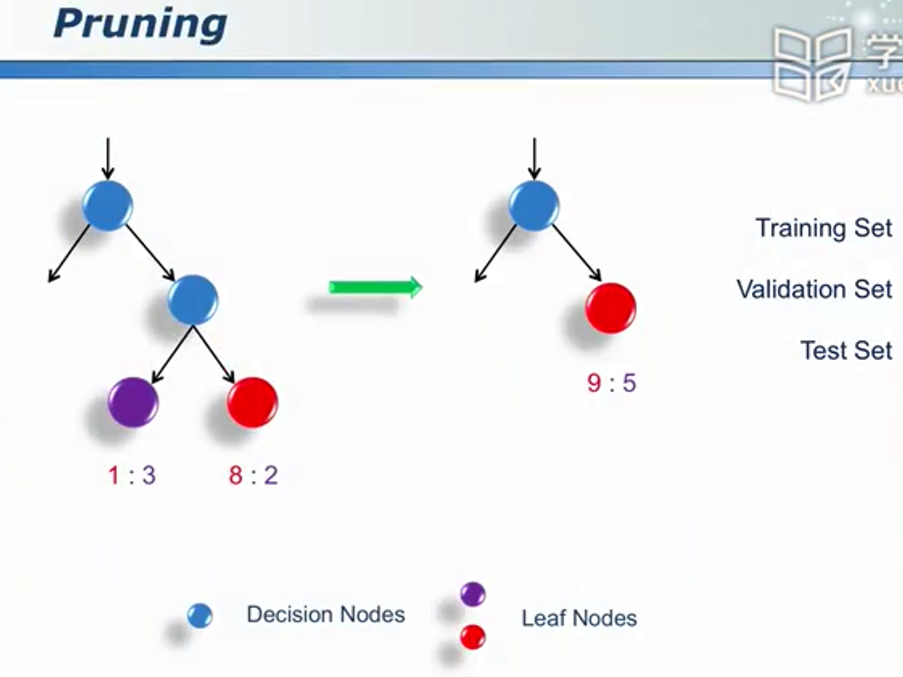
看着Validation的误差:先降低,后上升,要在即将上升的时候停下


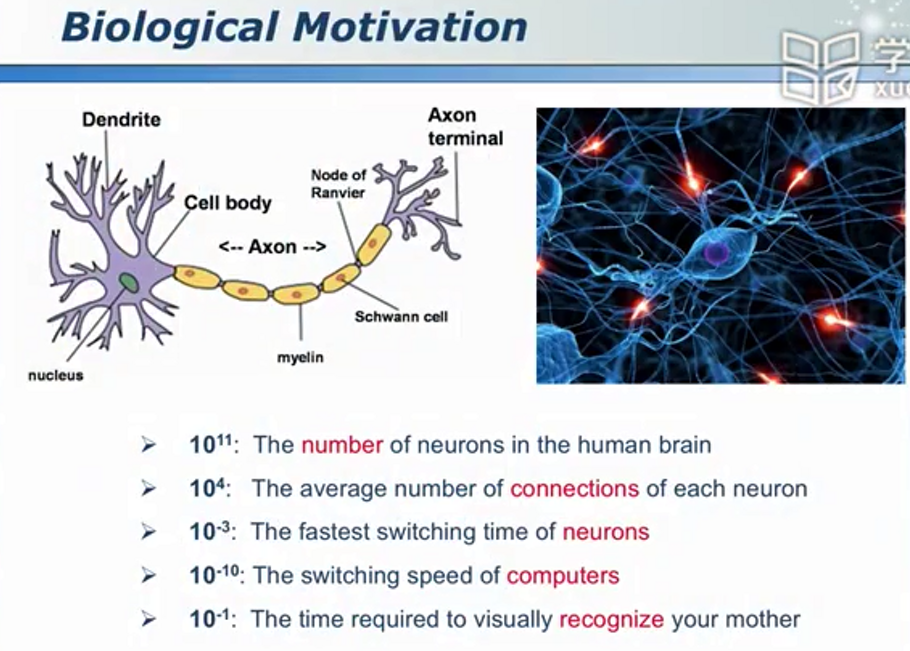
神经网络:巨量并行,智慧无限
智慧之源神经元
神经网络是一种和自然界联系紧密的分类器。其对大脑进行了高度的抽象和简化。


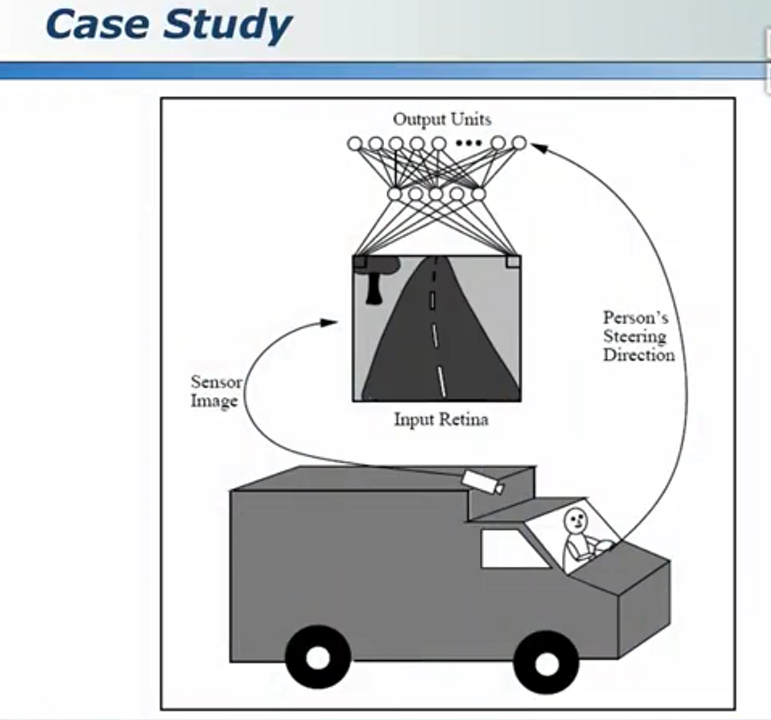
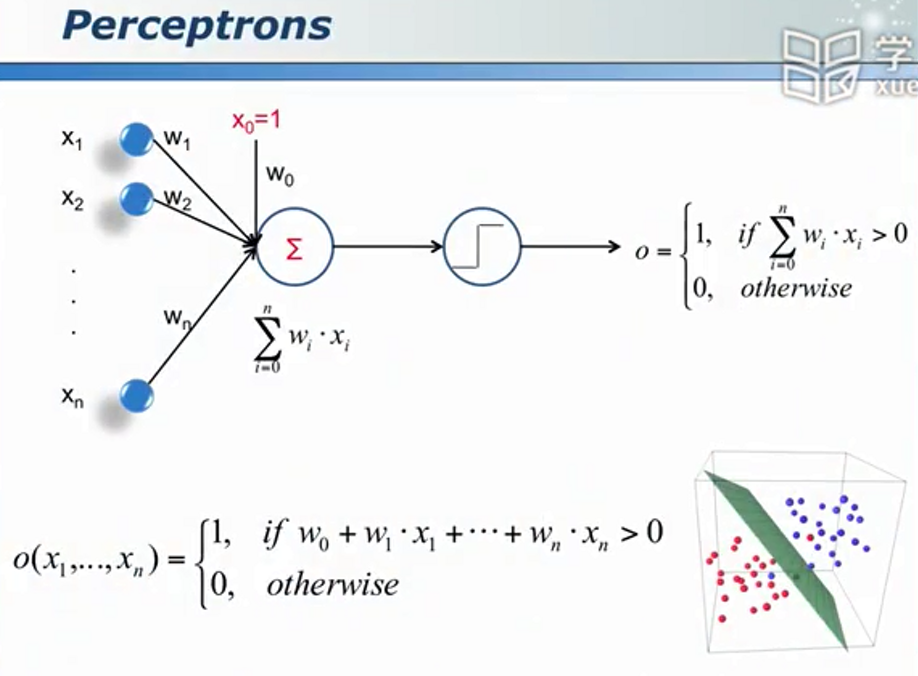
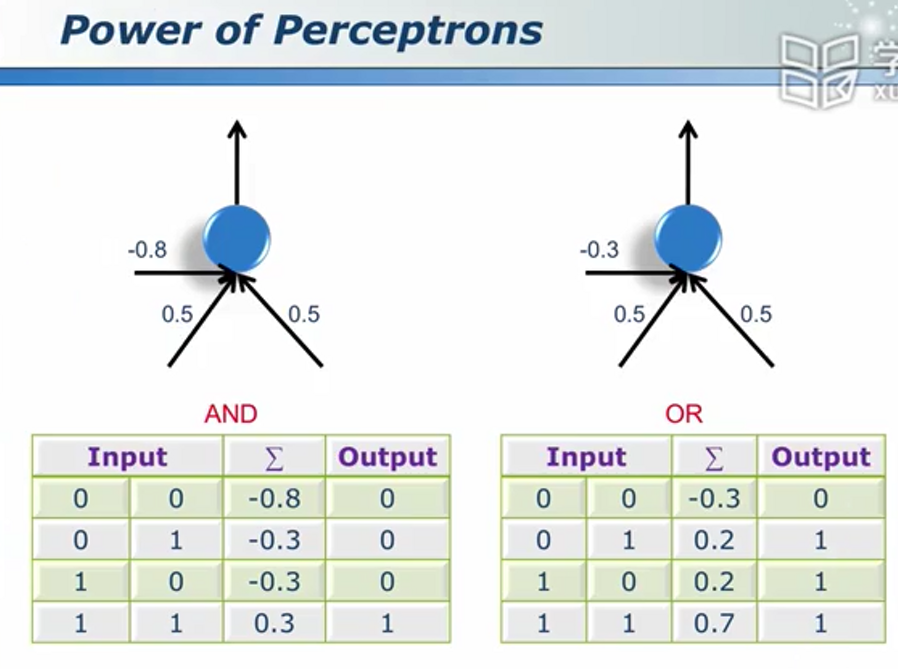
会学习的神经元
期望的效果
逐渐收敛到误差最小 的一个槽。
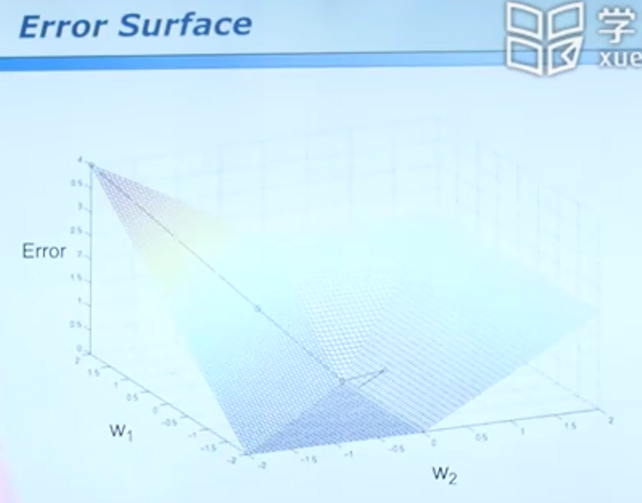
梯度下降法

在箭头所指公式上,随着w的增加,误差事实上会增加,若不加负号,则会减小,因此需要加上负号!
学习率用以控制每次修改的幅度。

写成算法



从一个到一群
多层感知机
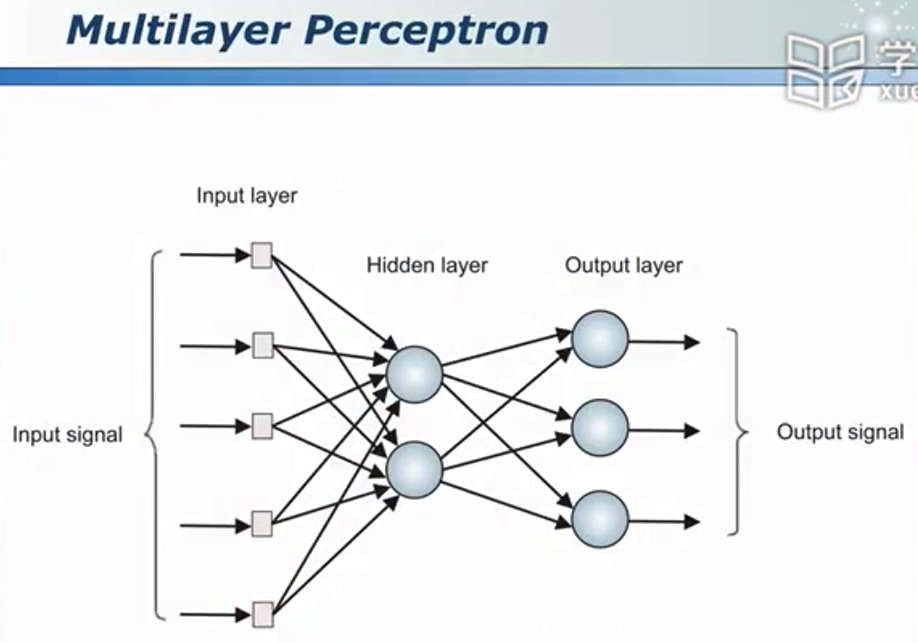
神经网络如何解决线性不可分问题


正向传播 --> 隐含层表示
(输入层p、q和输出层之间是线性不可分的,无法直接解决。我们可以先将其进行映射,映射到隐含层之后问题转变成为线性可分问题,再用一个即可将其分开)因此,隐含层的模式和其本身输入层的模式是不同的。这就是神经网络解决线性不可分问题的基本思想。
即:将原问题进行转化,使之成为一个相对容易的问题再进行解决。

Sigmoid函数
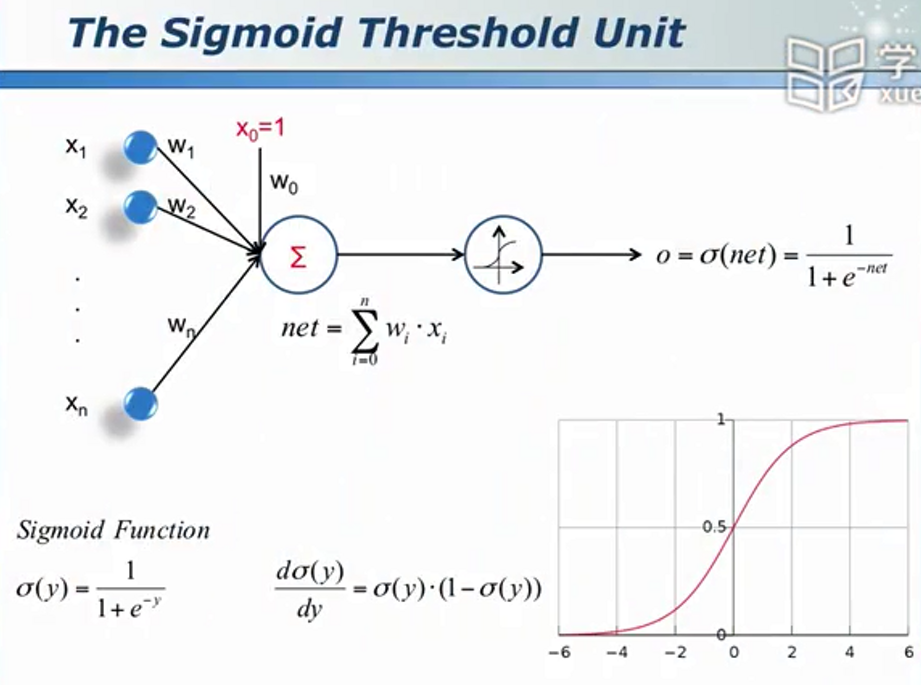
层次分明,责任到人
BP算法
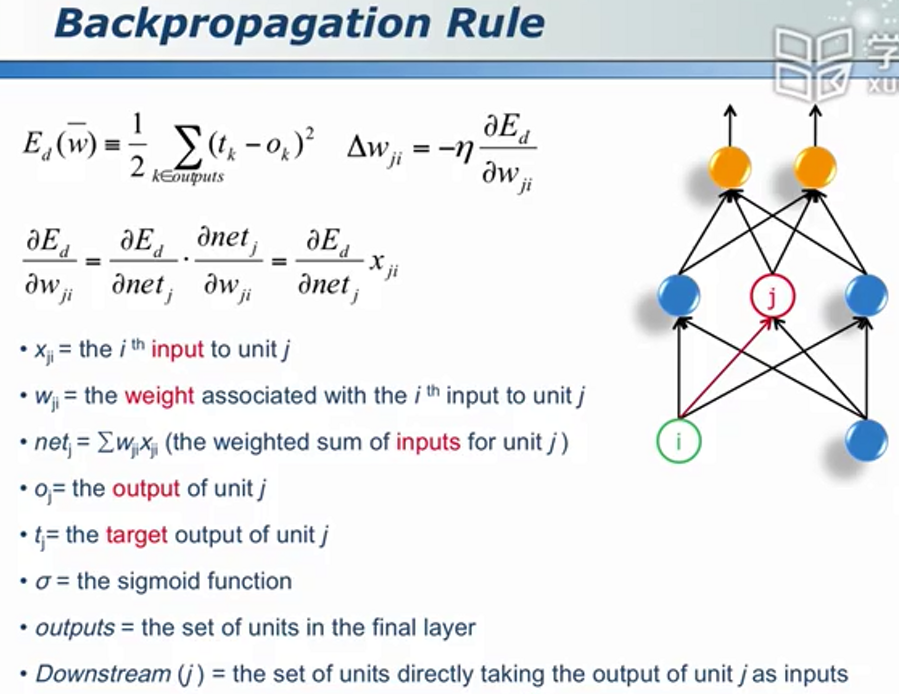
对于输出层神经元
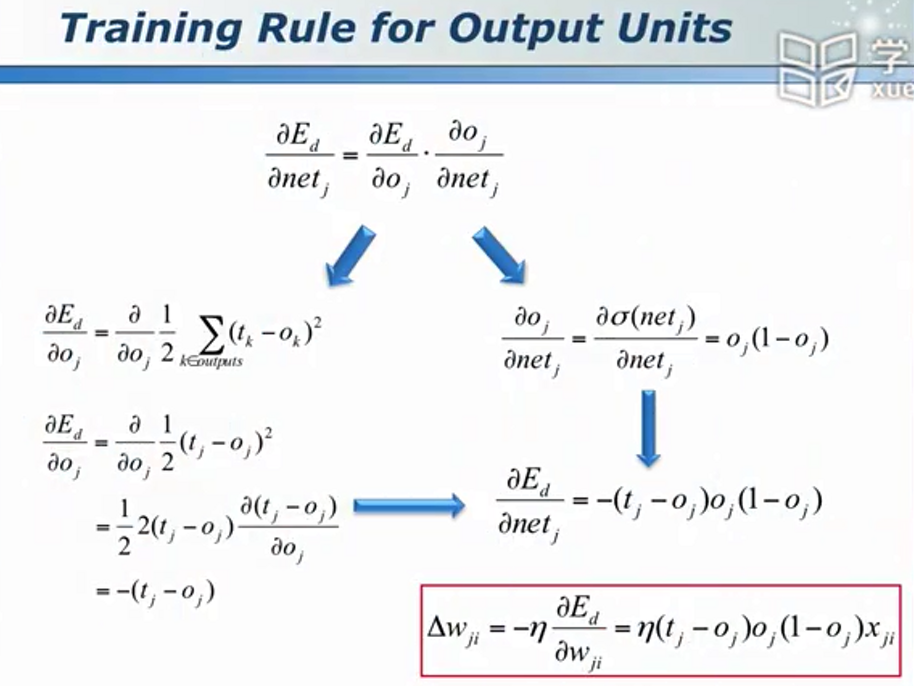
对于隐含层神经元 - 误差逆传播算法

框架结构



管中窥豹,抛砖引玉
Elman网络
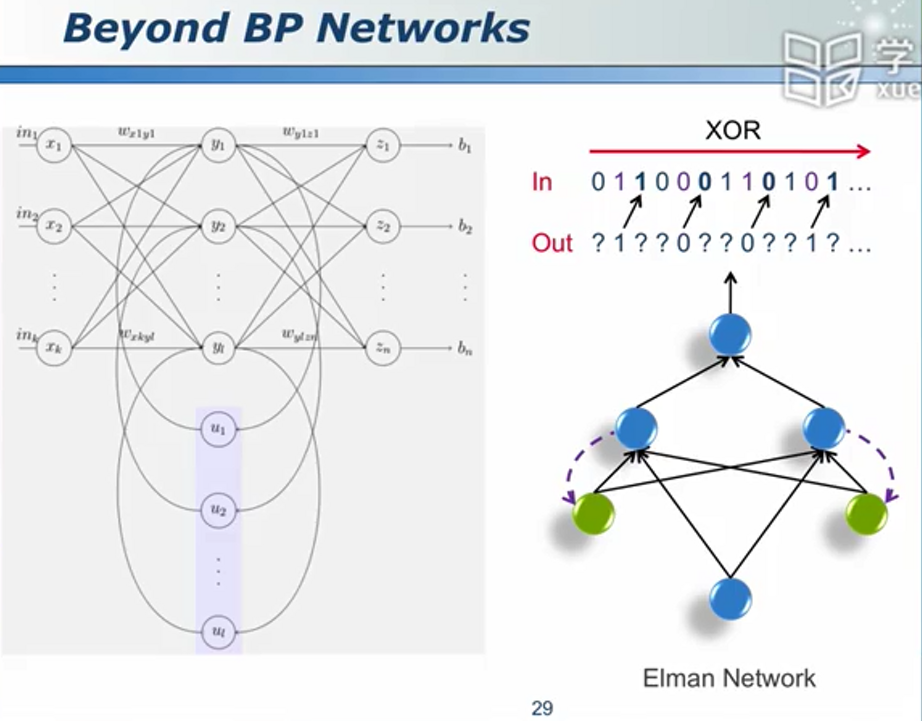
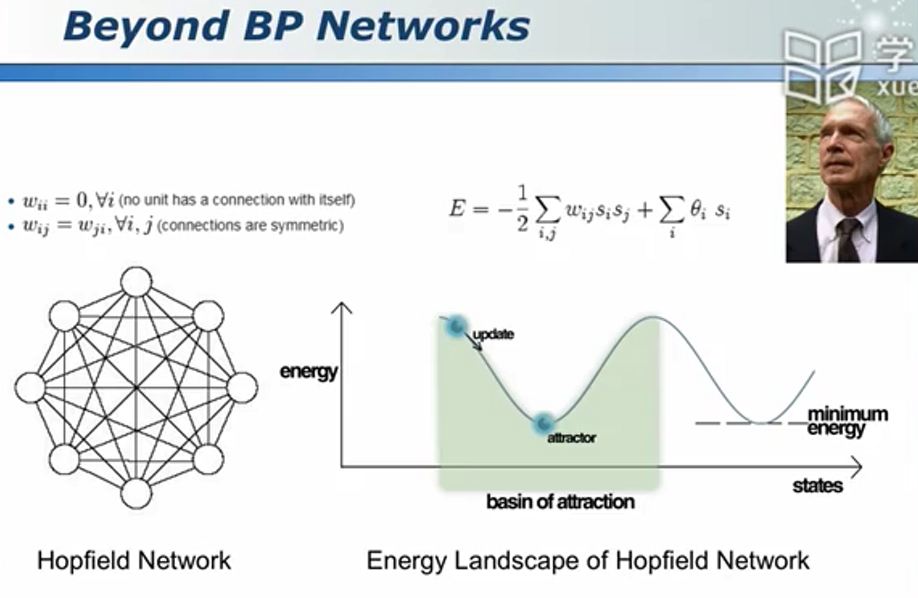
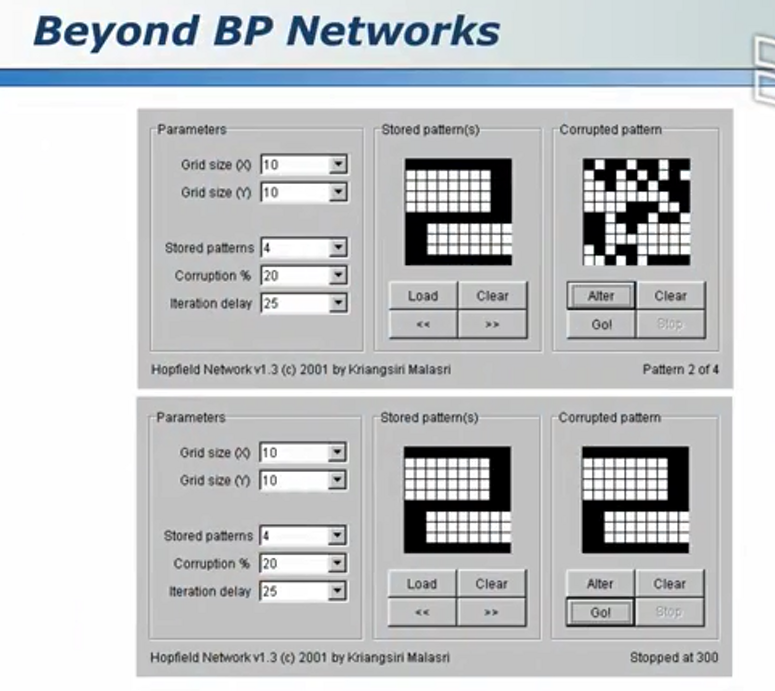
相对于决策树,神经网络的准确度较高,但是可解释度较差(因为神经网络的作用是权重)(例如你说这是一个苹果,但是怎么解释之?)


支持向量机:数学之美,巅峰之作
最大间隔
SVM概述

做了一个映射,在一个新的空间而不是原始空间做分类(目的使得原问题变为一个线性可分的问题)
线性分类器(Linear Classifier)
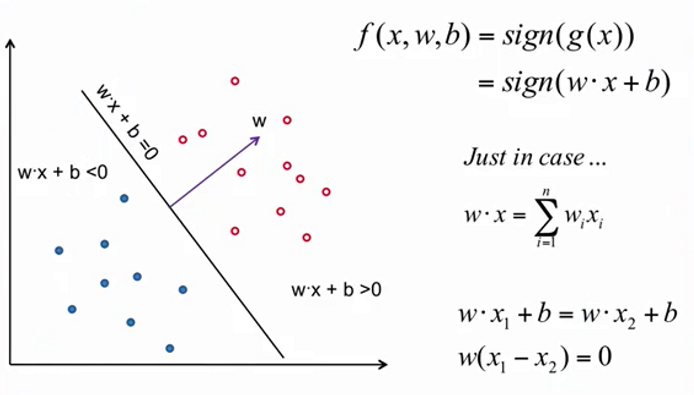
w是垂直方向
点到超平面的距离
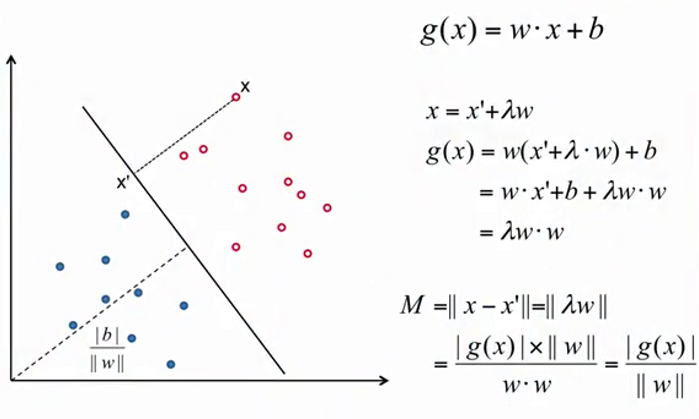
g(x)的绝对值比w的模,作为结论记忆
分类器的选择
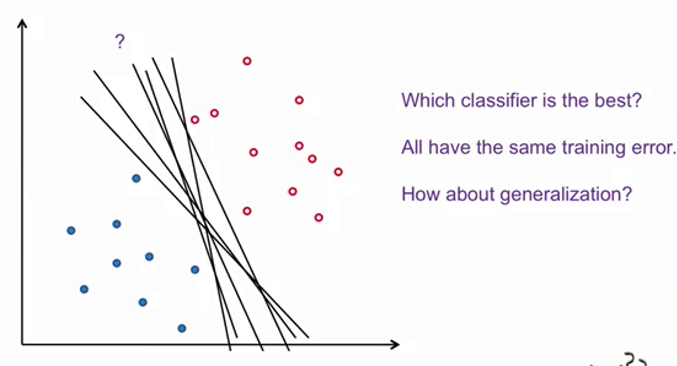
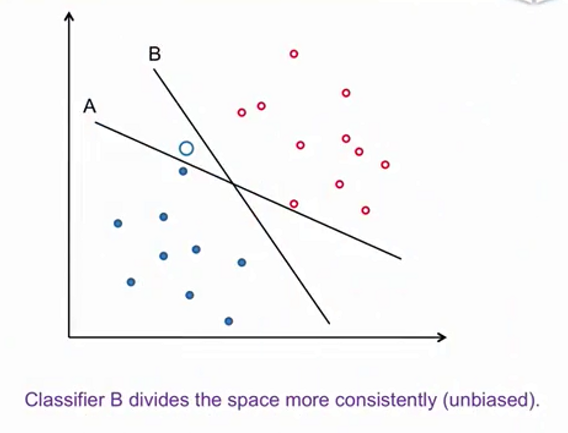
在上图中,我们认为分类器B更加合理(相对“无偏”)
Margin和Support Vectors
Margin用以描述分界面可以移动的空间范围,越大则代表其容错能力越强(越好)。
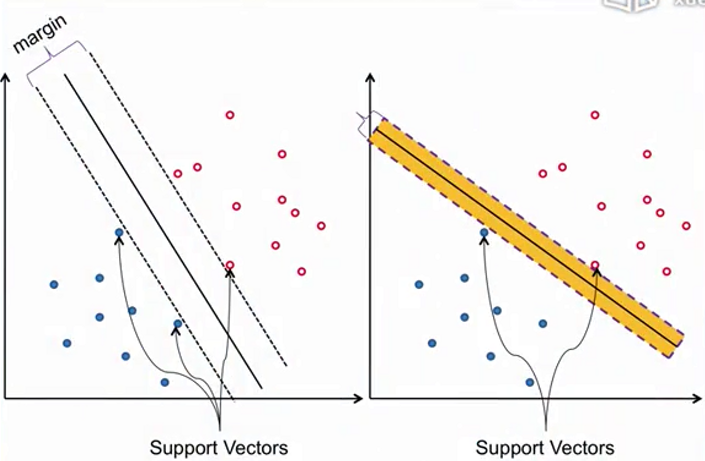
“支持向量”对于分界面起着“支撑”的作用

支持向量机最初就是一种线性分类器,其特殊之处在于可以最大化Margin(不仅能分对,而且使得Margin最大)
Margin的定量表达
只有定量表达优化目标,才能更加方便地优化它。
对于Margin,不妨借助点到超平面的距离公式来表达。
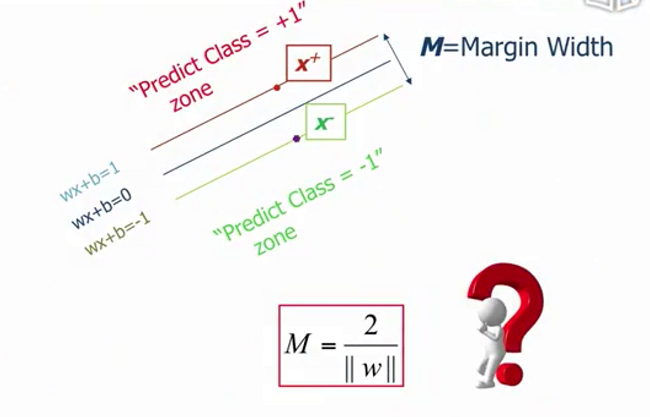
线性SVM
版权属于:soarli
本文链接:https://blog.soarli.top/archives/443.html
转载时须注明出处及本声明。

