一、简介
数学建模的核心
基本概念
什么是数学模型



数学结构

数学模型










数学建模的基本特征


方法步骤
数学建模的基本方法



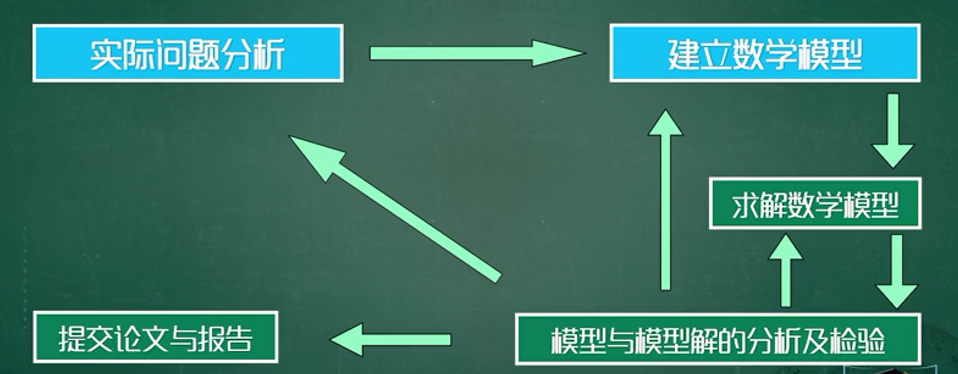
数学建模的步骤







模型系统性的作用


假设的合理性

合理假设应省遵循的原则

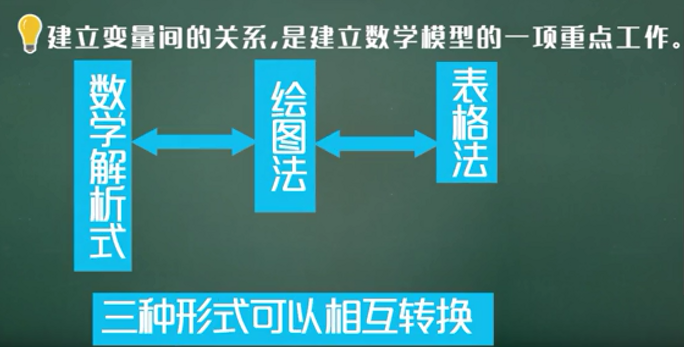
现实问题与数学表达式
数学建模的步骤


竞赛写作
国内外有哪些重要数学建模莞赛?

数学建模赛题形式


数学建模亮赛赛要求


数学建模评阅标准








论文写作结构


论文写作的注意事项


还有参考文献

科研素养

二、蛛网模型
问题提出与蛛网模型
市场经济中的蛛网模型的引入:
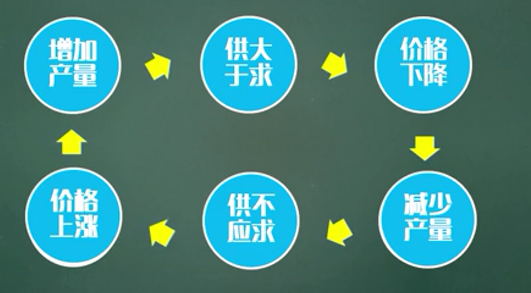
决策者往往希望数量和价格在一定范围内波动的良性循环。
为什么需要数量价格在一定范围内波动的良性循环额?
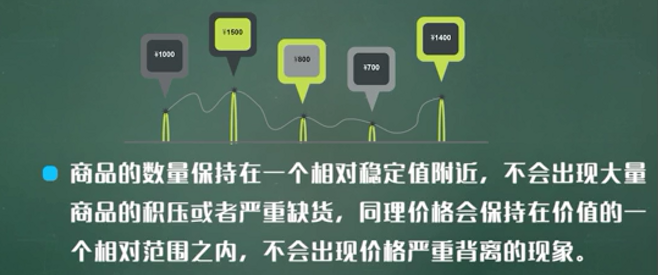

市场经济中的蜡网模型
目标:保持数量与价格之间的良性循环



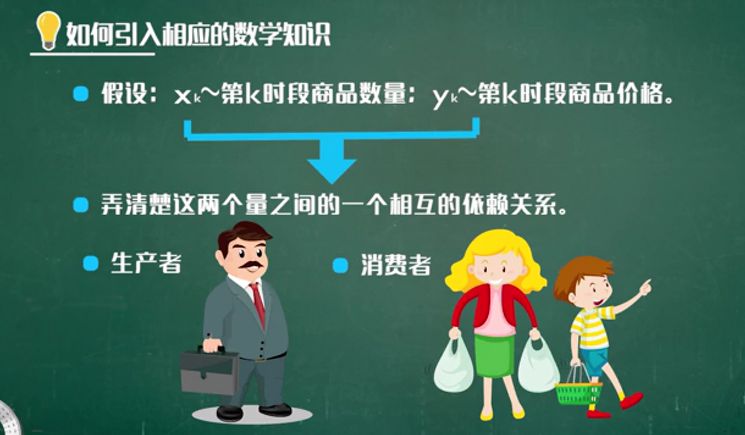

从单调性的角度考虑:
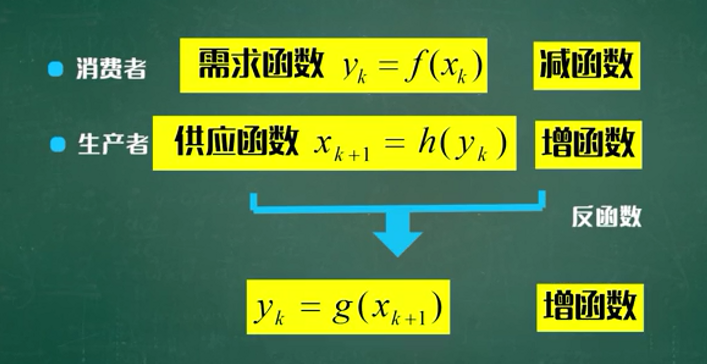


p1背离p0的情况:

上述两种情况(直观上的稳定与不稳定)在实际中都可能出现。
数学建模中,需要对该理论进行分析。
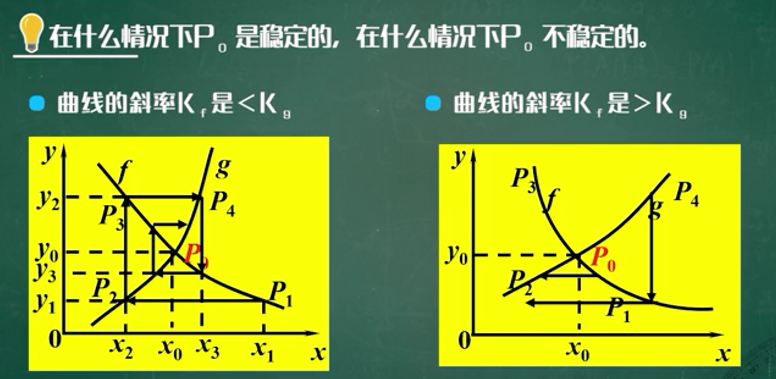
方程模型

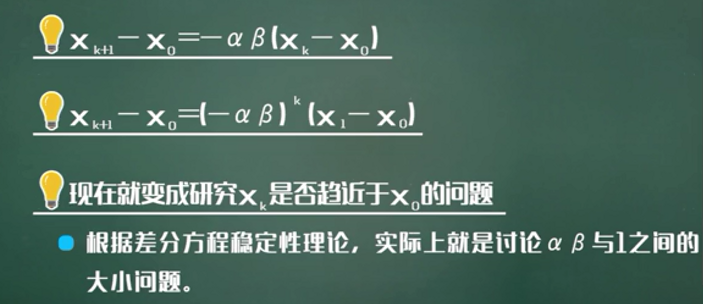


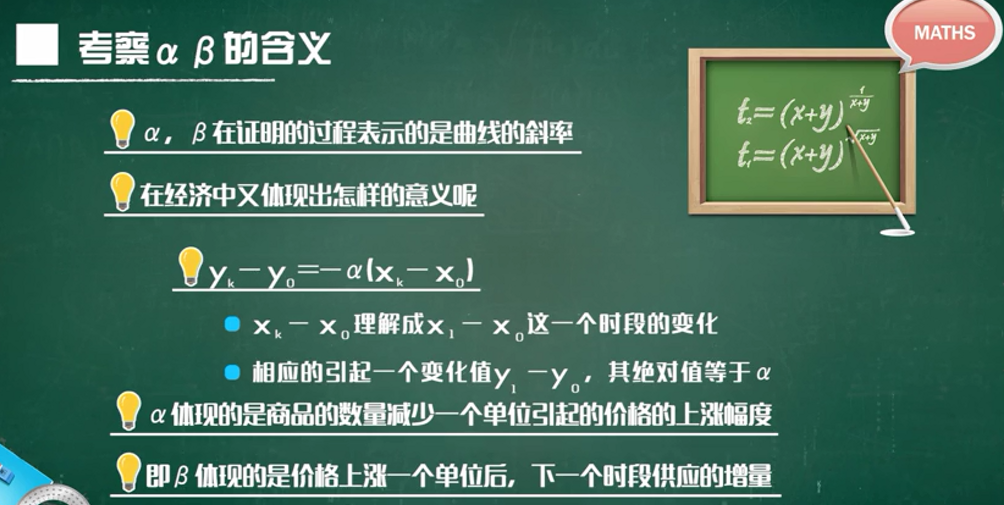




干预手段与模型推广
经济不稳定时决策者的干预办法



模型的推广







三、微分方程模型
引言
微分方程

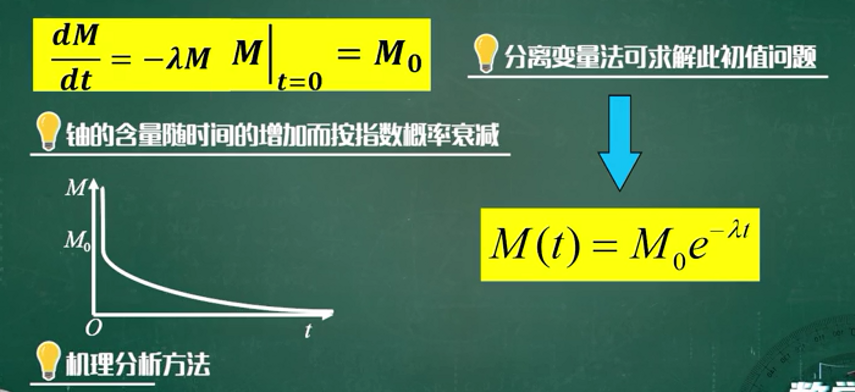
建模方法


人口模型



方程(2)是一个差分方程,可处理离散时间(如几年内)的人口数量情况。



指数增长模型
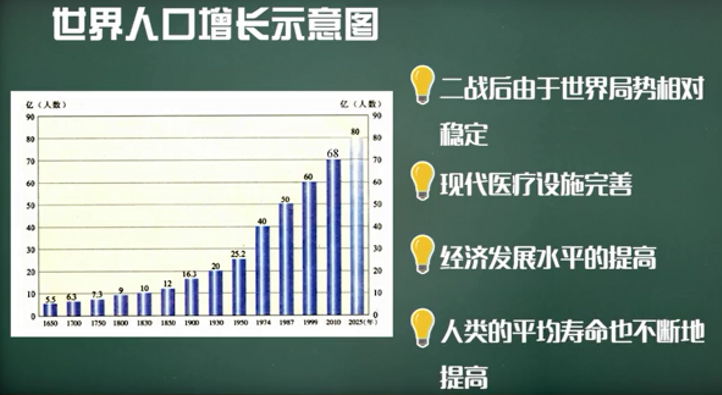
预报未来若千年的人口数


指数增长模型(Malthus模型)



模型求解


模型检验



马尔萨斯模型与19世纪以前欧洲一些地区人口统计数据吻合,可用于短期人口增长预测,不符合19世纪后多数地区人口增长规律。
阻滞增长模型
在马尔萨斯模型的基础上,考虑这个模型中度量人口增长率的比例因子k。

由此建立的模型叫做阻滞增长模型(Logistic模型)
阻滞增长膜型(Logistic模型)











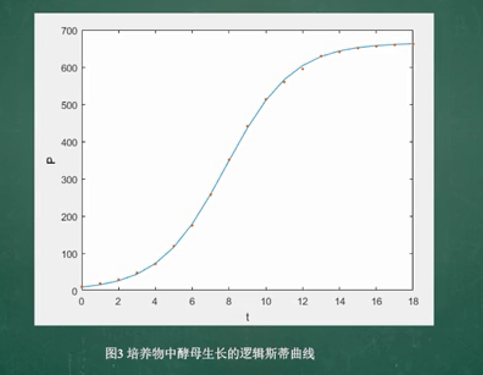

总结:logistic模型不仅适用于物种数量的变化规律,而且在社会经济领域也有广泛的应用。
年龄结构模型
指数增长模型和Logistic模型都不涉及年龄结构,接下来讨论年龄结构模型。
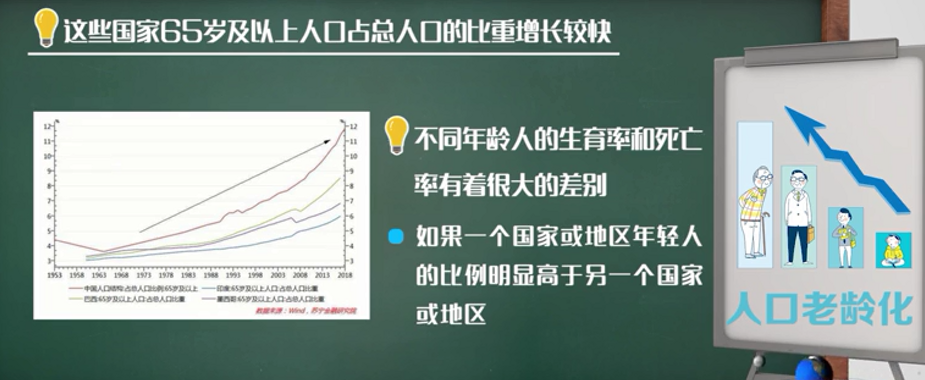
考虑年龄结构和生育模式的人口模型

人口发展方程

模型建立






人口控制




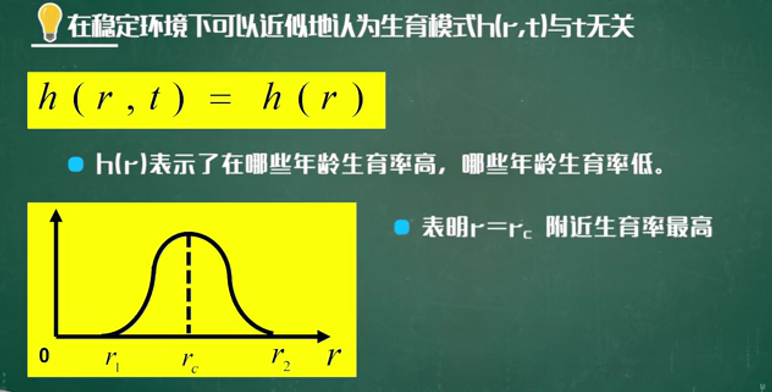

模型评价


模型应用


本节:只考虑自然的出生、死亡,不计迁移等社会因素的影响,建立了考虑年龄结构和生育模式的人口模型,最后讨论了模型的应用。
四、排队模型
实例与问题
在日常生活中,因为人数众多等原因,排队的现象很常见

如何缩短和优化排队等候的时间?

排队实例与问题


概念与原理
什么是排队系统?


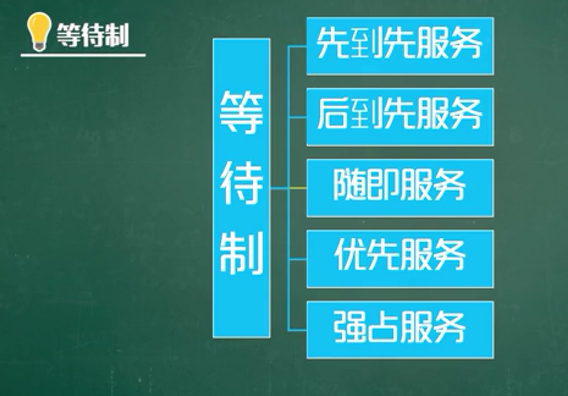

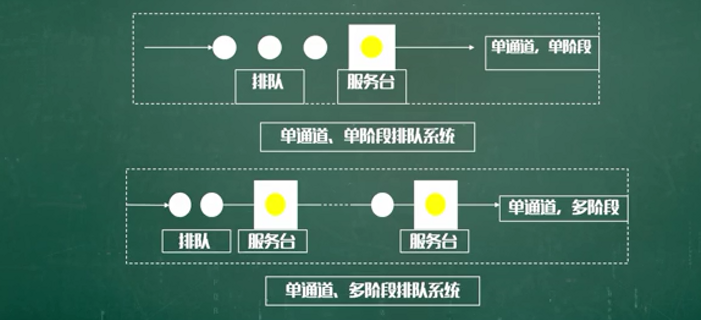
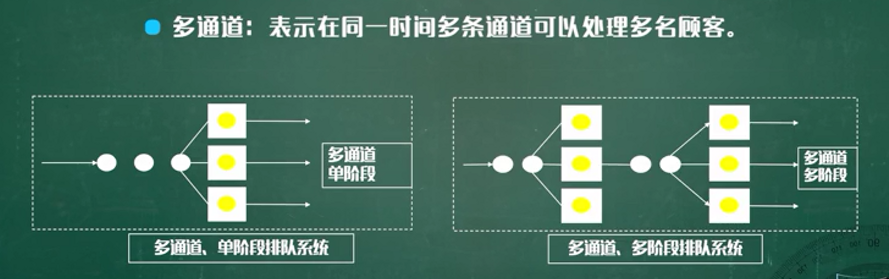
排队模型的几个步骤


游乐场排队建模
案倒分析--游乐园排队:快速通过系统(FP)

模型的假设

第一个假设:fp系统统计之后,计算出顾客返回的时间间隔或时间点或时间窗。
第二个假设:
第三个假设:

第四个假设:

泊松过程(Poisson Process)


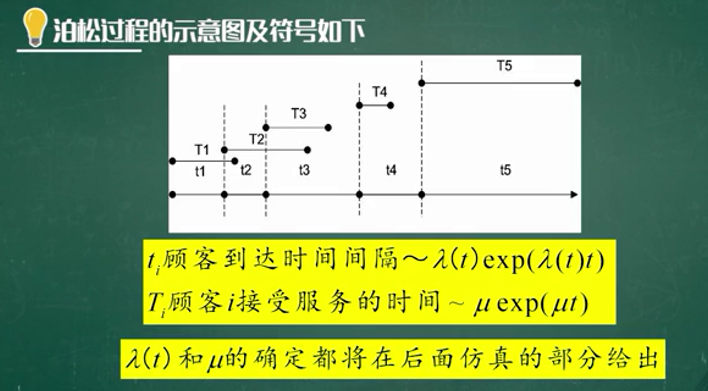
问题分析



模型1的建立-目标函数



模型2-边山车排队模型



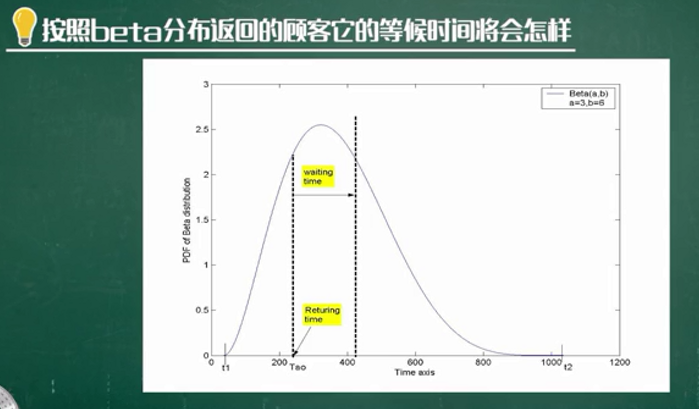
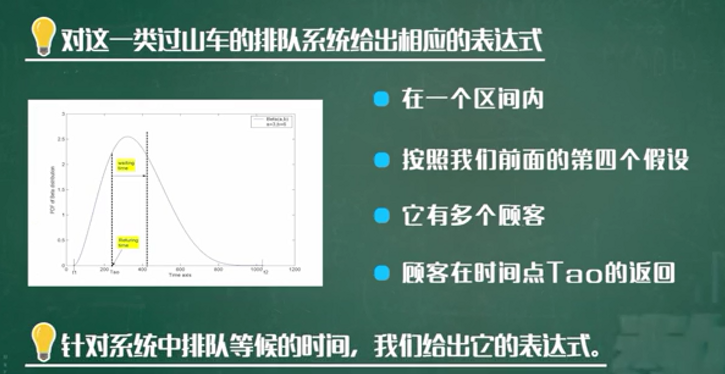




求解与改进
模型2的求解-边山车模型


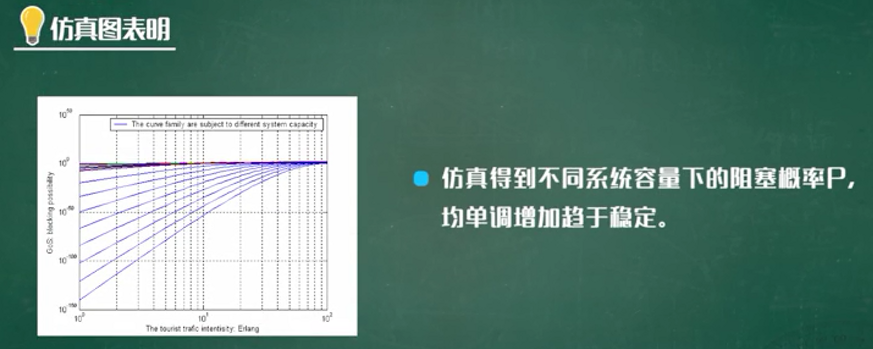
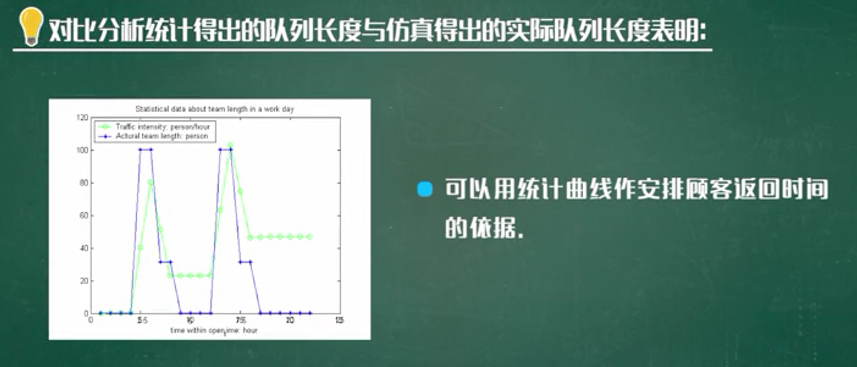
过山车模型的仿真



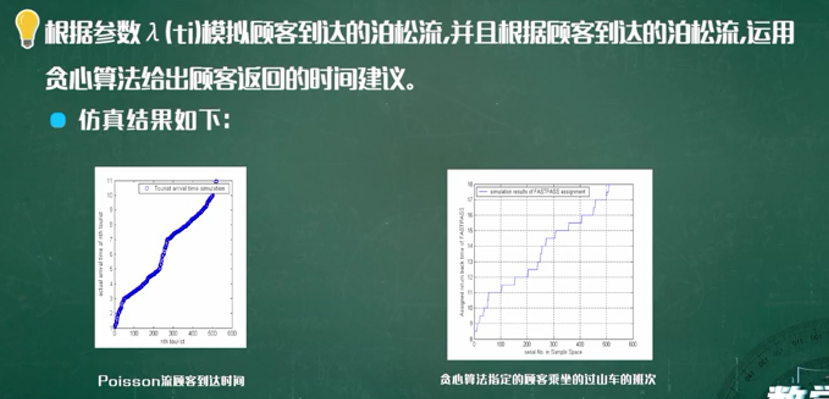
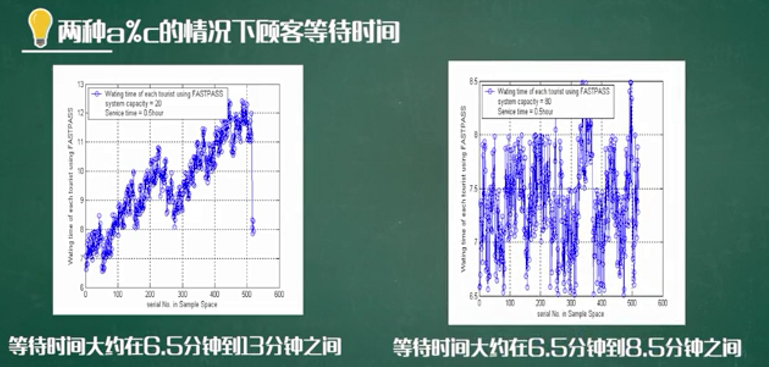
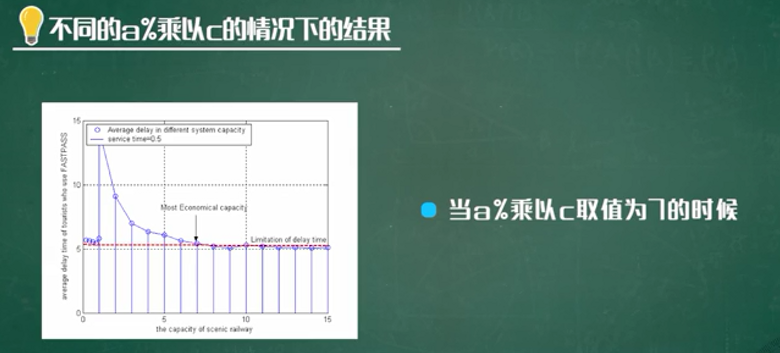
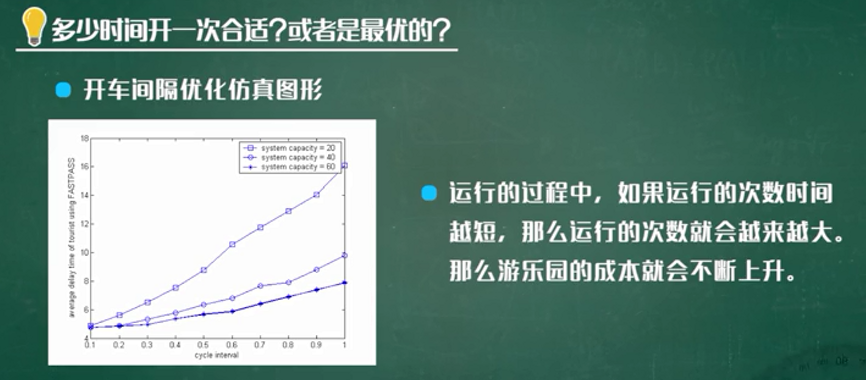
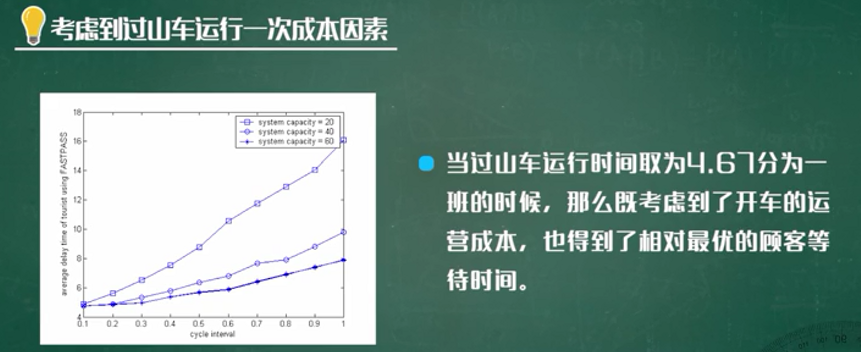
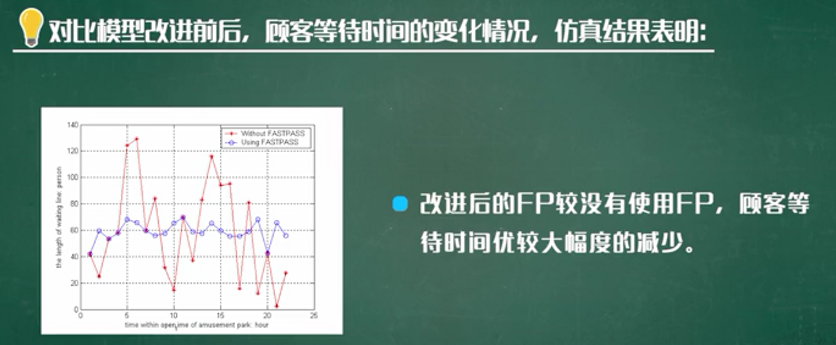
模型的改进



五、线性规划模型
问题提出与线性规划模型
规划模型的一般形式

厂长最关心的问题:技术问题?规模问题?人工问题?
生产计划中的线性规划模型

实际问题





生产计划问题的表格形式
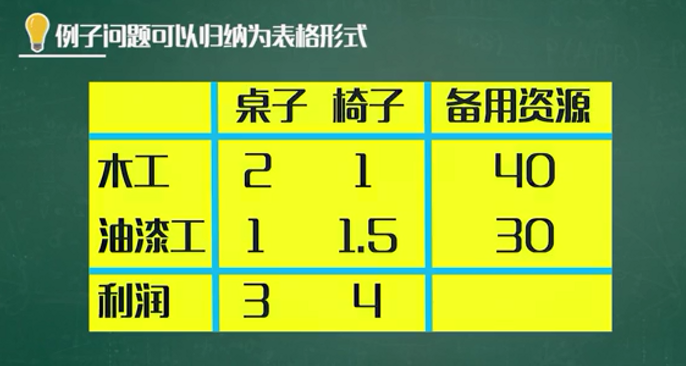
家具生产的例子

规划模型是在一组限制条件下求函数的最大/小值问题。
线性规划模型特点及标准形式问题

线性规划模型的一般式

模型规范与图解法
线性规划模型的标准型(standard model)

非规范性模型转换为规范型模型步骤



把线性规划模型化为标准型

于是,原规划问题转换成为如下标准型

线性规划求解--图解法


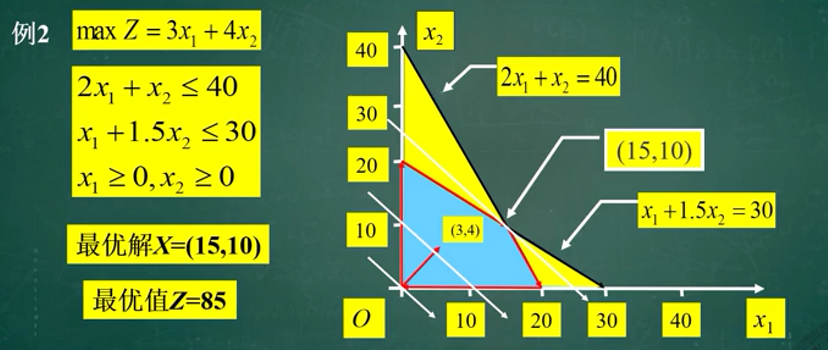
单纯形法求解

线性线性规划求解--单纯形法(Dantzing,1947)

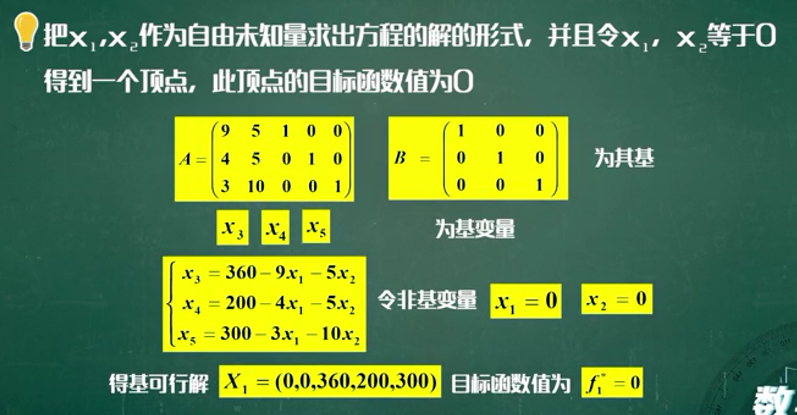



用MATLAB优化工具箱解线性规划



一个例子:

六、动态规划模型
动态规划的基本概念
动态规划是解决多阶段决策过程最优化的一种方法,该方法将一系列较难的多阶段决策问题化为一系列简单的单阶段决策问题。
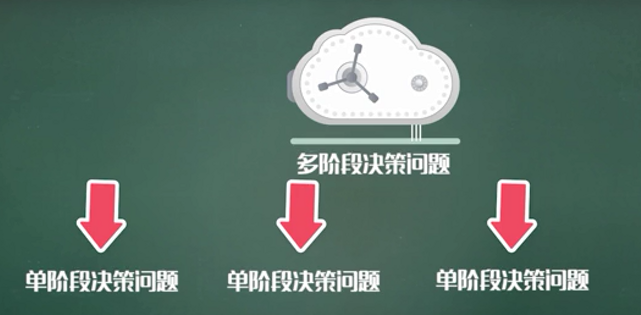
其中,多阶段决策问题概念如下:

用动态规划模型可以解决的问题:
基本概念











一、阶段
把所要处理的问题合理地划分成若干个相互联系的阶段,通常用K表示阶段变量。
二、状态和状态变量

三、决策和决策变量

四、策略和子策略


五、状态转移方程



六、指标函数和最优指标函数


动态规划的原理
最优性原理

动态规划的数学模型



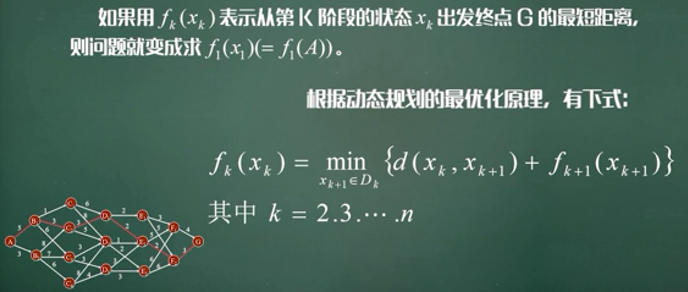
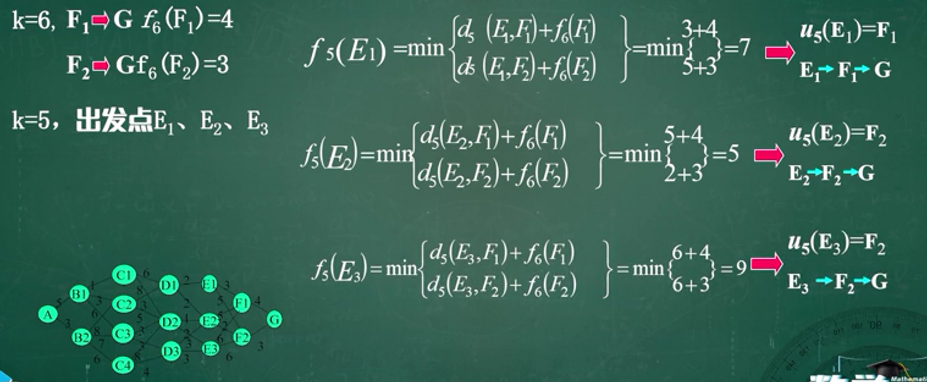

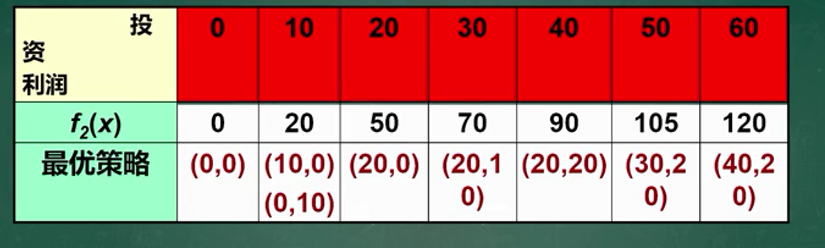
投资分配问题


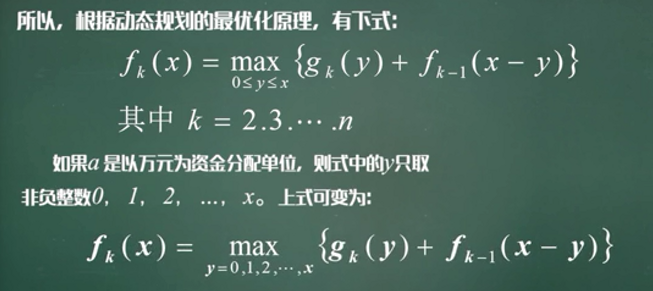
案例一
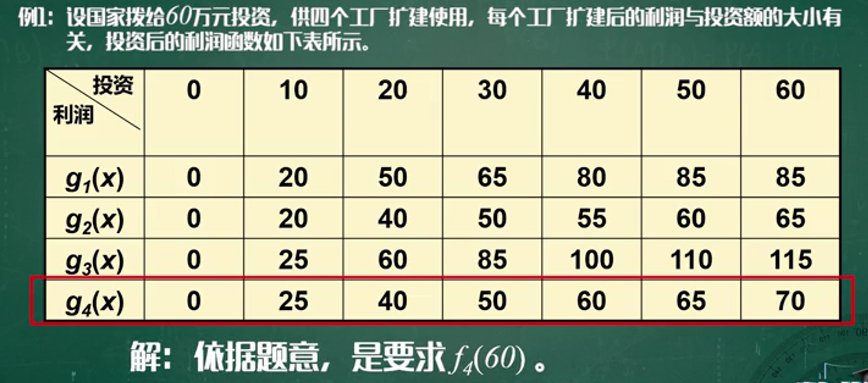
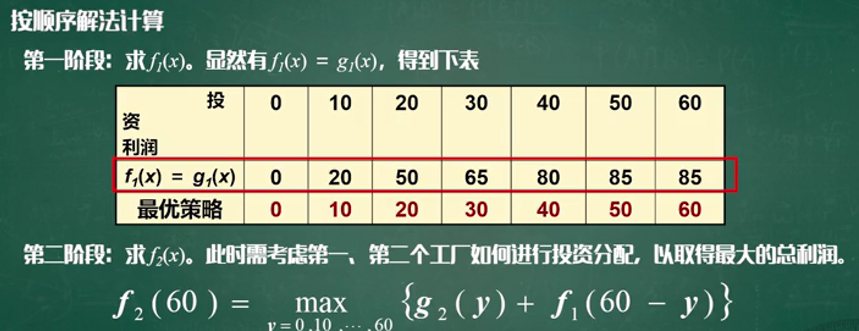

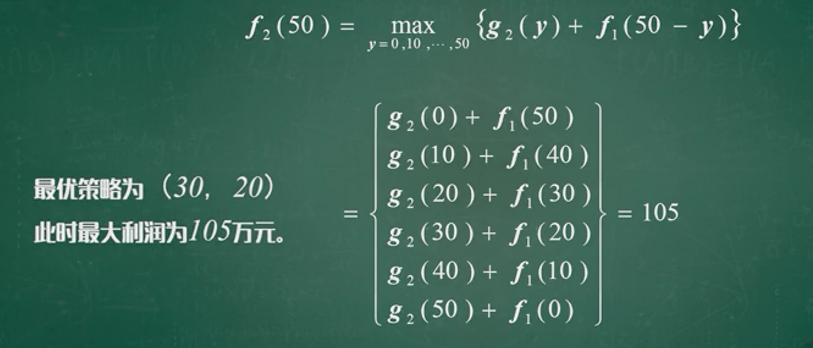
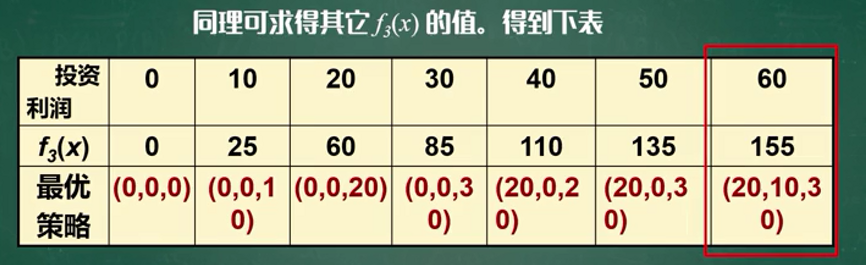
同理可求出:




背包问题
旅行者携带物品问题:
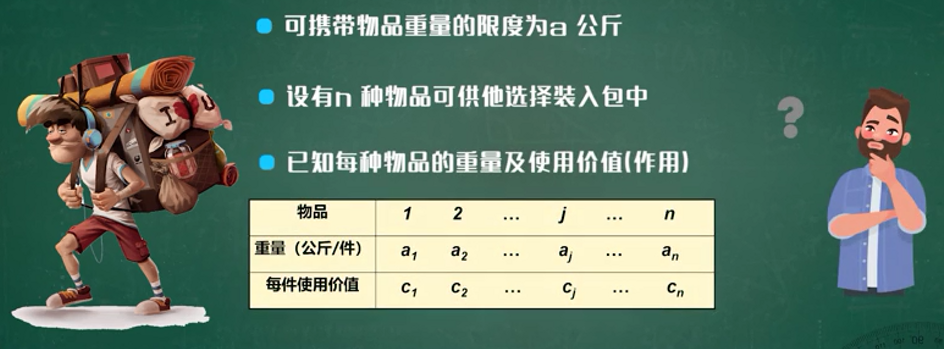
问:此人应如何选择携带物品的件数,使其作用最大?

工厂里的下料问题,运擒中的货物装载问题,人造卫星内的物品装载问题等同样属于背包问题!


求背包问题的最优解
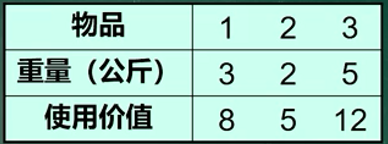



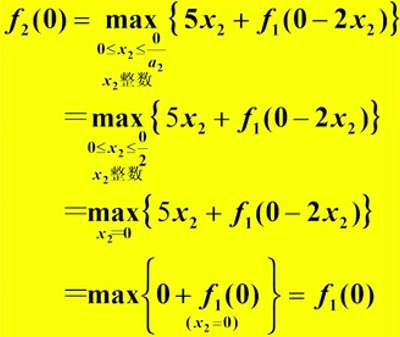
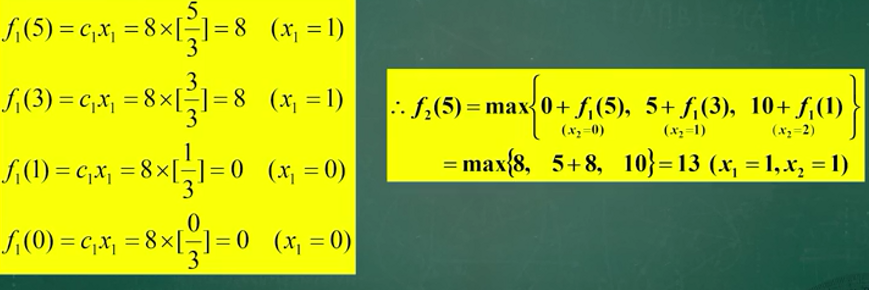

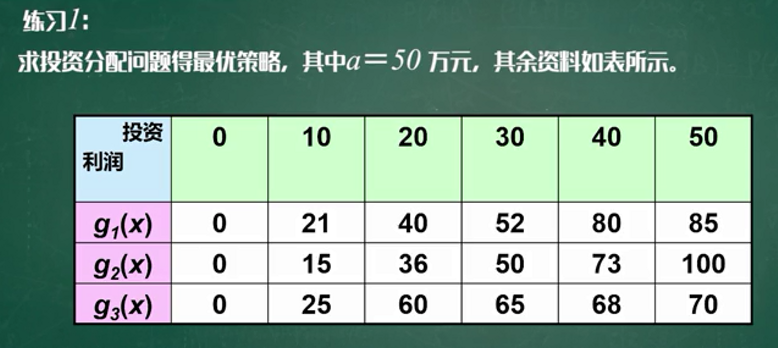
仿照背包问题求解练习题
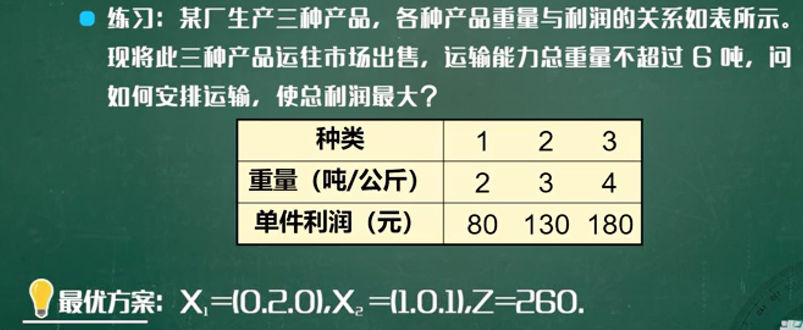
动态规划算法与贪心算法的区别
贪心算法:
1.贪心算法中,作出的每步贪心决策都无法改变,因为贪心策略是由上一步的最优解推导下一步的最优解,而上一部之前的最优解则不作保留。
2.由(1)中的介绍,可以知道贪心法正确的条件是:每一步的最优解一定包含上一步的最优解。动态规划算法:
1.全局最优解中一定包含某个局部最优解,但不一定包含前一个局部最优解,因此需要记录之前的所有最优解
2.动态规划的关键是状态转移方程,即如何由以求出的局部最优解来推导全局最优解
3.边界条件:即最简单的,可以直接得出的局部最优解贪心法的基本思路:
从问题的某一个初始解出发逐步逼近给定的目标,以尽可能快的地求得更好的解。当达到某算法中的某一步不能再继续前进时,算法停止。
该算法存在问题:
1. 不能保证求得的最后解是最佳的;
2. 不能用来求最大或最小解问题;
3. 只能求满足某些约束条件的可行解的范围。实现该算法的过程:
从问题的某一初始解出发;while 能朝给定总目标前进一步 do
求出可行解的一个解元素;
由所有解元素组合成问题的一个可行解贪心算法最经典的例子,给钱问题。
比如中国的货币,只看元,有1元2元5元10元20、50、100如果我要16元,可以拿16个1元,8个2元,但是怎么最少呢?
如果用贪心算,就是我每一次拿那张可能拿的最大的。
比如16,我第一次拿20拿不起,拿10元,OK,剩下6元,再拿个5元,剩下1元
也就是3张 10、5、1。每次拿能拿的最大的,就是贪心。
但是一定注意,贪心得到的并不是最优解,也就是说用贪心不一定是拿的最少的张数
贪心只能得到一个比较好的解,而且贪心算法很好想得到。
再注意,为什么我们的钱可以用贪心呢?因为我们国家的钱的大小设计,正好可以使得贪心算法算出来的是最优解(一般是个国家的钱币都应该这么设计)。如果设计成别的样子情况就不同了
比如某国的钱币分为 1元3元4元
如果要拿6元钱 怎么拿?贪心的话 先拿4 再拿两个1 一共3张钱
实际最优呢? 两张3元就够了求最优解的问题,从根本上说是一种对解空间的遍历。最直接的暴力分析容易得到,最优解的解空间通常都是以指数阶增长,因此暴力穷举都是不可行的。
最优解问题大部分都可以拆分成一个个的子问题,把解空间的遍历视作对子问题树的遍历,则以某种形式对树整个的遍历一遍就可以求出最优解,如上面的分析,这是不可行的。
贪心和动态规划本质上是对子问题树的一种修剪。两种算法要求问题都具有的一个性质就是“子问题最优性”。即,组成最优解的每一个子问题的解,对于这个子问题本身肯定也是最优的。如果以自顶向下的方向看问题树(原问题作根),则,我们每次只需要向下遍历代表最优解的子树就可以保证会得到整体的最优解。形象一点说,可以简单的用一个值(最优值)代表整个子树,而不用去求出这个子树所可能代表的所有值。
动态规划方法代表了这一类问题的一般解法。我们自底向上(从叶子向根)构造子问题的解,对每一个子树的根,求出下面每一个叶子的值,并且以其中的最优值作为自身的值,其它的值舍弃。动态规划的代价就取决于可选择的数目(树的叉数)和子问题的的数目(树的节点数,或者是树的高度?)。
贪心算法是动态规划方法的一个特例。贪心特在,可以证明,每一个子树的根的值不取决于下面叶子的值,而只取决于当前问题的状况。换句话说,不需要知道一个节点所有子树的情况,就可以求出这个节点的值。通常这个值都是对于当前的问题情况下,显而易见的“最优”情况。因此用“贪心”来描述这个算法的本质。由于贪心算法的这个特性,它对解空间树的遍历不需要自底向上,而只需要自根开始,选择最优的路,一直走到底就可以了。这样,与动态规划相比,它的代价只取决于子问题的数目,而选择数目总为1。
来源:https://blog.csdn.net/HerosOfEarth/article/details/52374337
七、图论模型
图论基本概念
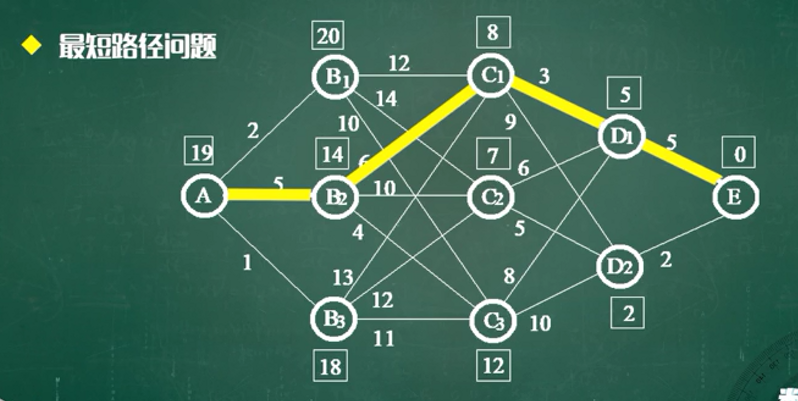
生活中有很多图论的应用问题,如:路径导航/最短路径问题。
图论的基本概念





距离矩阵

例如:矩阵A就是左图的距离矩阵。

指定两点最短路算法


Dijkstra算法

算法步骤

案例





MATLAB程序

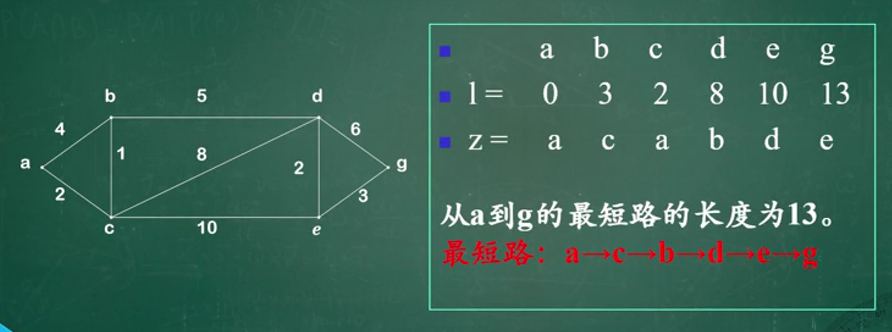
任意两点最短路算法


Floyd-Warshal算法



算法原理


算法描述



多阶段决策的图论模型
例子
企业设备损耗,选择维修还是重新购置?
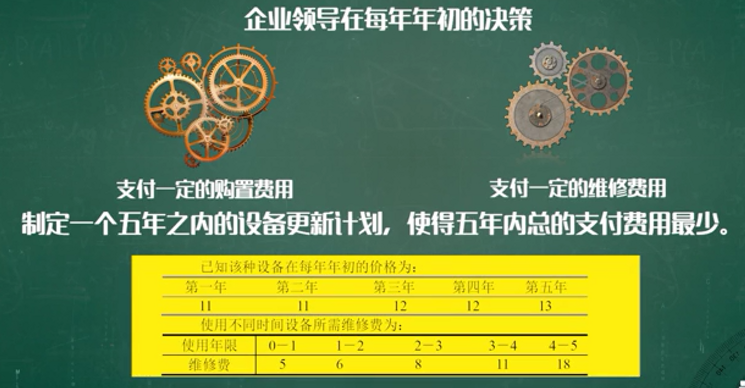
有向图



版权属于:soarli
本文链接:https://blog.soarli.top/archives/461.html
转载时须注明出处及本声明。

