雨中走路淋雨多还是跑步淋雨多？

前言

雨中走路淋雨多还是跑步淋雨多？记得我很小的时候就思考过这个问题，到了中学阶段又借助所学知识思考过，最后结论是“如果一个人行走的速度无限慢，那么他淋的雨量趋近于无穷大；如果他行走的速度无限快，那么他淋的雨量趋近于一个恒定值”，也就是走得越快，淋雨越少。

今天偶然看到了“李永乐老师微信公众号”推送了一篇关于这个问题的文章，较为系统的分析了“淋雨”的过程。个人觉得写的不错，将其原文在博客记录之（已在文末注明来源）。

转载

如果有一天下雨了，你刚好没有带伞，还没有地方避雨，那么你会选择在雨中漫步还是奔跑呢？

这是一个古老的问题，引起了国内外的数次讨论。中央电视台《加油向未来》节目还做了个实验，得出了跑步淋雨少的结论。国外的节目《流言终结者》也做了实验，而且做了两次，居然得到了相反的结果。

原因在于，这个问题在实际中影响因素非常多，例如雨量、风速、人的速度、人的表面积和形状等等，都会影响实验结果。尤其是如果雨滴下落时不均匀，那么随机性就会变得更大。

01

物理模型

我在这里基于简单的物理模型做一个分析。所谓物理模型，就是从一个实际的复杂问题中抽象出最核心的内容，而忽略其他不重要的影响因素。例如我们研究地球围绕太阳运动，就把地球看作一个点，而不去管地面上的山川河流，这就是质点模型。作为一个模型，我们必须给出一些假设，虽然这些假设可能与实际情况并不完全相同。

假设1：雨是均匀的，雨滴无限小而且各处密度均匀，单位体积内雨的质量为ρ。

假设2：没有风，雨滴匀速下落，速度为v。

假设3：人匀速运动，运动的速度为u。

假设4：把人的身材看作一个长方体，人身体前方的面积为S1，头顶的面积为S2。

假设5：人的目标是从A地到达相距L的B地。

有了以上假设，我们就可以进行计算了。人在雨中向前运动，头顶会淋雨，前面也会淋到雨。我们要分别计算这两部分。

02

基本分析

我们首先要研究的是空间中哪些雨落在了人的身上。如果选取地面作为参考系的话，人在运动，雨也在运动，问题会比较复杂。我们可以换一个参考系——以人为参考。这样一来，人就可以看作静止不动的，而雨滴在竖直方向具有下落的速度v，在水平方向具有相对于人向后的水平速度u，雨滴相对于人就是斜向下运动的，如图所示↓

人从A地到B地的过程中，雨滴相对于人向斜下方匀速直线运动，能够落到人身上的雨滴（忽略人头顶的一个小三角形）都在他斜前方一个柱体内，如图中的ACDE部分。这些雨滴会朝着人奔跑，最终撞到人身上。

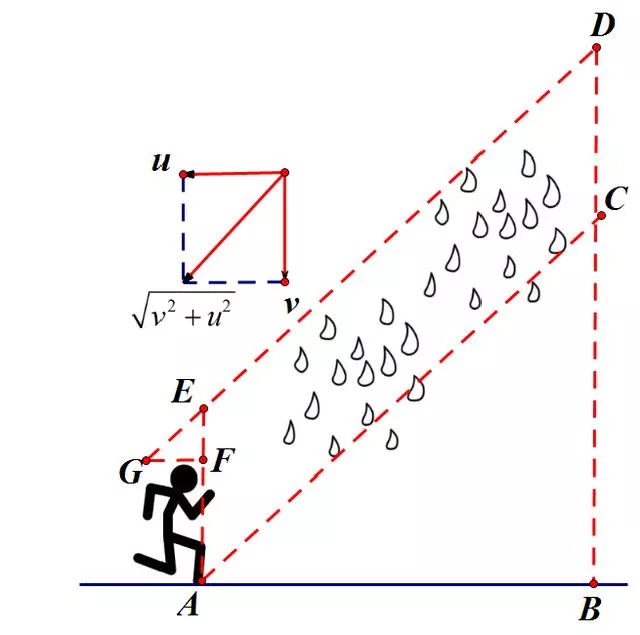
这是一个斜柱体，它的底面积是人迎接雨滴的截面积S，如图中AE部分所示；而柱体的高是AB之间的距离AB=L。根据柱体体积公式得到雨滴体积V=SL，单位体积的雨滴质量为ρ，于是最终落到人身上的雨滴的总量为：m=ρSL。

03

如何淋雨少？

那么，如何才能淋雨更少呢？

显而易见，无论以多大速度奔跑，AB之间的距离L是一定的。当奔跑速度不同时，雨滴相对于人的速度不同，因而柱体的倾斜程度不同，截面积S不同。

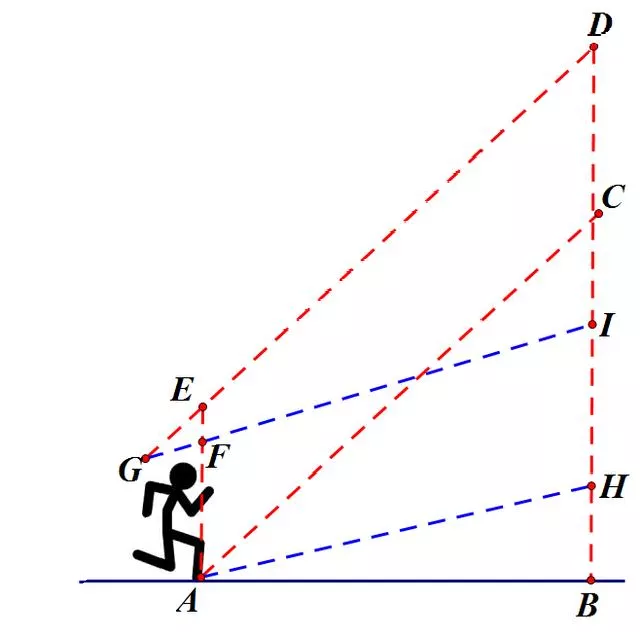
如上图所示，如果人的奔跑速度比较大，雨滴相对于人速度更接近水平，这样人迎接雨滴的截面积为AF部分；如果人的奔跑速度比较小，雨滴相对于人速度方向更加竖直，人迎接雨滴的面积是AE部分。

显然，柱体AFIH和柱体AEDC的高相同，但是AF部分面积更小，柱体体积更小，柱体中的雨质量更小，即人以更大速度奔跑时，淋雨少。如果人以无限大的速度奔跑，则雨滴一点也不落到头顶，而是全部落在人的身体前侧面。

04

还能再给力一点吗？

那么，如果人已经达到最大奔跑速度了，还有没有可能继续减少淋雨呢？

其实我们还有办法。因为人的头顶面积小于身体前面的面积，我们可以让身体倾斜过来，迎接雨滴，这样就可以使得人迎接雨滴的面积进一步减小，雨柱体变得更细。

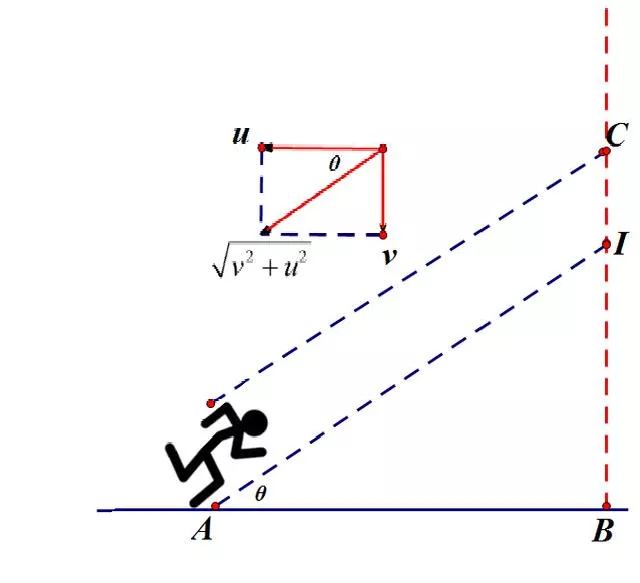
如果要获得最小的迎接雨的底面积，就应该完全用头顶面积迎接雨，此时人的倾斜程度应该与雨相对于人的速度方向平行。如图所示，这个夹角用三角函数表示就是：

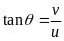
比如人的奔跑速度和雨滴下落速度相同时，人向前倾斜45度角是最好的。

综上所述，在一定的模型条件下，人以尽量大的速度奔跑，并且使身体向前倾斜，可以使落到身上的雨滴减少。如果我们可以精巧地调整身体的角度，使得总是只有头顶迎接雨滴，那么我们只需要一小块挡住脑袋的荷叶，就可以保证身上一点水都没有。

原文地址：

https://mp.weixin.qq.com/s/hIV0mQVmZGUrMICadPx-1Q

版权属于：soarli

本文链接：https://blog.soarli.top/archives/566.html

转载时须注明出处及本声明。