数值分析课堂笔记

第1章 数值分析与科学计算

1.1数值分析的对象作用与特点

一、什么是数值分析

数值分析是计算数学的一个主要部分，计算数学是数学科学的一个分支，它研究用计算机求解各种数学问题的数值计算方法及其理论与软件实现。

实际问题→数学模型→数值计算方法→程序设计→上机计算求出结果

数值分析的基本内容

1、数值逼近

• 插值法
• 函数逼近与曲线拟和
• 数值积分与数值微分

2、数值代数

• 线性代数问题（方程组和特征值）
• 非线性方程（组）数值解法

3、常微方程数值解法和偏微方程数值解法（如神经网络）

二、计算数学与科学计算

现代科学的三个组成部分：

科学理论，科学实验，科学计算

科学计算的核心内容是以现代化的计算机及数学软件（Matlab，Mathematica，Maple，MathCAD etc.）为工具，以数学模型为基础进行模拟研究。

促使一些边缘学科的相继出现：
计算数学，计算物理学，计算力学，计算化学，计算生物学，计算地质学，计算经济学，等等.

三、数值问题与算法

目的：
理论可靠、计算复杂性好和能在计算机上实现的求解数学模型方法。

• 理论可靠：稳定性、收敛（快慢）性。
• 计算复杂性好：时间、存储开销。
• 计算机上可实现：有限（可操作）性。
• 计算机软、硬件的发展为数值方法的实现提供环境，也促进它的快速发展.

数值分析的特点：

1、面向计算机

2、可靠的理论分析，保证收敛性、稳定性

3、良好的计算复杂性

4、数值实验

四、如何学好数值分析

1、注意掌握基本原理、处理技巧，误差分析

2、注重实际问题，练习、作业

3、积极动手上机实践

五、数值分析解决的问题

1.2数值计算的误差

一、误差来源、分类

模型误差：
从实际问题建立的数学模型往往都忽略了许多次要的因素，因此产生的误差称为模型误差.

观测误差：
一般数学问题包含若干参数，它们是通过观测得到的，受观测方式、仪器精度以及外部观测条件等多种因素的影响，不可能获得精确值，由此而来产生的误差称为观测误差。

截断误差或方法误差:
数值方法求出的近似解和精确解之间的误差

舍入误差

由于计算机字长有限，原始数据在计算机上表示时所产生的误差

二、近似数的误差和有效数字

三、数值运算的误差估计

随堂练习：

1.3误差定性分析、避免误差危害

一个算法，如果在执行它的过程中舍入误差在一定条件下可以得到控制（或者说初始误差和舍入误差的增长不影响产生可靠的结果），则称它是数值稳定的，否则称该算法数值不稳定。

尝试使用两种算法来解决它：

显然，算法A是失败的。

分析：

避免误差危害的若干原则：

除了分清算法是否数值稳定外，还要考虑避免误差危害和防止有效数字损失的如下原则.

第2章 插值法

2.1 引言

一、问题背景

函数逼近：

• 数学中的基本问题，最活跃的研究领域之一
• 数值计算中函数表示的重要方法

本质是讨论如何用

• 简单函数近似代替复杂函数
• 简单函数曲线拟合离散数据的方法、理论及其实现

现代机械工业中用计算机程序控制加工机械零件，根据设计可以给出零件外形曲线的某些节点，加工时为了控制每步走刀方向和步数，就需要算出零件外形曲线，才能加工出外形光滑的零件，这其实就是插值函数的问题。

二、一般概念

三、多项式插值函数的唯一性

2.2拉格朗日插值

一、线性插值和抛物插值

几何意义：给定两点，确定一条直线

因此，

二、拉格朗日插值多项式

为了简便，

三、插值余项与误差估计

2.3差商与牛顿插值

一、差商及其性质

拉格朗日插值优缺点：

• 优点：公式紧凑，插值基函数，性质一目了然，在理论分析中甚为重要
• 缺点：当插值节点增加时，计算需要全部推倒重来，非常麻烦

为此，引入牛顿插值多项式：

考察：

差商：

差商的基本性质：

性质一：

衍生性质：

2.4习题课

2.4差分与等距节点插值

上节讨论任意分布节点的插值公式，应用时常碰到等距节点的情形，此时插值公式可简化，为此先介绍差分。

一、差分及其性质

二、等距节点插值公式

由于牛顿插值多项式：

2.5埃尔米特插值

不少插值问题不仅要求在节点上函数值相等，而且要求在某些节点上对应的的导数值甚至高阶导数值相等.这种插值问题称为埃尔米特（Hermite）插值问题

证明方法：

当n=l时，应用广泛的三次埃尔米特插值多项式：

拉格朗日插值多项式及其余项与埃尔米特插值多项式及其余项的比较

怎么根据插值条件构造出插值多项式

拉格朗日插值多项式

如果有n+1个节点：

满足：

埃尔米特插值多项式

怎么分析误差（两种插值多项式的余项）

根据插值条件构造出插值多项式并分析出它的插值余项（误差），是本章重要的两个内容。

拉格朗日插值多项式

埃尔米特插值多项式

2.6分段低次插值

一、高次插值的病态性质

那么，是不是对于插值多项式来说次数越高误差越小呢？

龙格现象

例子：

两等分三节点

其中，黑色的曲线表示目标函数，红色的曲线表示抛物插值多项式（二次插值多项式）

可以看到，误差较大。

尝试增加节点的个数：

四等分5节点

蓝色的曲线表示四次插值多项式

八等分9节点

10等分11节点

即便用10次，误差依然比较大：

原因？

当n趋于无穷时，上式的分子和分母都增大。

二、分段线性插值

当h->0时，误差也趋近于0.

三、分段三次埃尔米特插值

即：一阶导数连续

即：Ih（x）必须满足插值条件

即 在三个小区间上都必须是一个埃尔比特插值多项式

它在整个区间a，b上是一阶导数连续的。

接着分析三段三次埃尔比特插值多项式的误差：

2.7样条插值

分段低次插值函数具有一致收敛性，但是光滑性较差。比如分段线性插值多项式只能保证连续性，不能保证可导性；分段埃尔米特插值多项式只能保证一阶导数连续。对于像高速飞机的机翼形线要求二阶导数连续以减小空气阻力。

一、样条插值的概念

再加上插值条件，共4n-2个条件（3n-3）+(n+1).

我们需要确定4n个待定系数，因此还差两个条件，通常在两个端点加上边界条件.

二、三次样条插值函数的建立

求三次样条插值函数常用三弯矩法和三转角法.

带入之后可以确定两个待定系数c1，c2.

和前面n-1个方程联立，可以得到一个n+1阶的线性代数方程组，通过求解可以得到M0~Mn的值。

因此我们只需要求解n-1阶的线性微分方程组。

第4章数值积分和数值微分

4.1 引言

一、数值求积的基本思想

回顾求积分的方法：

二、代数精度的概念

定义1：
若一个求积公式对于所有次数不超过m的多项式都准确成立，而对于某一个m+1次的多项式等式不准确成立，则称该求积公式具有m次代数精度。

当求积节点个数给定后，怎样构造数值求积公式？

成立。

如何构造求积公式？

模式一：给定节点，系数待定。

模式二：节点、系数全待定

三、插值型求积公式

四、求积公式的收敛性和稳定性

4.2 牛顿-科特斯系数

一、Newton-Cotes公式的导出

一、Newton-Cotes公式的代数精度

定理3：若n为偶数,则n阶N - C公式至少有n+ 1次代数精度。

三、几种低阶Newton-Cotes求积公式的余项

1. 梯形公式的余项

2.辛普森公式的余项

4.3 复化求积公式

一、复化梯形公式，

二、复化辛普森公式

4.4龙贝格求积算法

一、梯形公式的递推化（变步长求积法）

由于被积函数的原函数不能用初等函数表示出来，所以我们只能采用数值积分法。

二、龙贝格公式

编程思想：

三、理查森外推加速方法

4.5高斯求积公式

一、一般理论

只要求解：

二、高斯-勒让德求积公式

第5章解线性代数方程组的直接法

5.1引言与预备知识

一、引言

• 线性方程组的来源

• 线性方程组的分类

  • 低阶稠密矩阵
  • 大型稀疏矩阵

二、线性方程组的两类解法：

1. 直接法（由于舍入误差的存在，只能求得线性方程组的近似解）
2. 迭代法（用某种极限过程去逼近线性方程组精确解，存在收敛性和收敛速度的问题）

回忆线性代数知识点：

1. 矩阵加法
2. 矩阵的数乘
3. 矩阵的乘法
4. 矩阵的转置
5. 非奇异矩阵
6. 矩阵的行列式
7. 矩阵的特征值和特征向量

三、特殊矩阵

1）对角矩阵

2）三对角矩阵

3）上三角矩阵

4）上海森伯（Hessenberg）阵

5）对称矩阵

6）埃尔米特矩阵

7）对称正定矩阵

8）正交矩阵

9）西矩阵

10）初等置换阵

11）置换阵

5.2高斯消去法

一、高斯消去法

说明：
若线性方程组的系数矩阵非奇异（行列式不等于0），则它总可以通过带行交换的高斯消去法进行求解。

二、矩阵的三角分解

下面建立高斯消去法与矩阵的因式分解的关系.

...

证分解方法的唯一性：

5.2第一次实验课（Matlab介绍）

Matlab除了不能生孩子，什么都能干！

Matlab能干啥？

图像处理：

生成音频：

人脸识别与图像优化：

生成小游戏：

概括：

Matlab可用其验证算法，使用C/C++实现。

Matlab中定义的变量都是“矩阵”类型（数字是1*1的矩阵）

常用命令：

三角函数与四则运算：

若不指定结果存放的变量，则使用默认ans变量：

清屏命令：clc

定义行/列向量：

定义矩阵：

求矩阵的逆：

用C的思路：定义一个3*6的矩阵，用高斯消去...

matlab：

求矩阵的行列式：

矩阵的运算：

A+10表示A的每一个元素都加10：

每一个元素取正弦值：

矩阵的转置：

不妨验证一下：

若要显示小数点后更多位：

显示更少位：

矩阵的乘法：

和python不同，python默认为对应元素相乘，matlab默认矩阵相乘。

若要实现对应元素直接相乘，只需加“.”：

同理，每个元素平方：

取倒数：

矩阵的连接：

复数的引入：

复数域下的矩阵：

其他：

效果：使得行列对角之和都是34（想到了数独）

矩阵元素的引用：

引用第一行/列：

1-3行中2-4列的值：

生成1-10：

类似python

生成奇数：

生成随机数：

保存数据：

调用保存的数据：

5.3高斯主元素消去法

列主元消去法

算法（列主元消去法）

5.4矩阵的三角分解法

2、选主元直接三角分解法

二、平方根法

应用有限元法解结构力学问题时，最后归结为求解线性代数方程组，系数矩阵往往对称正定。平方根法是一种对称正定矩阵的三角分解法，广泛用于求解系数矩阵为对称正定的线性代数方程组。

设A为对称矩阵，且顺序主子式不为零，则

三、解三对角方程组的追赶法

第7章解非线性方程的迭代法

7.1方程求根与二分法

一、引言

二、二分法

7.2迭代法

一、不动点迭代

二、不动点的存在性与迭代法的收敛性

三、局部收敛性与收敛阶

7.3迭代收敛的加速方法

一、埃特金加速收敛方法

二、斯蒂芬森迭代法

7.4牛顿法

一、牛顿法及其收敛性

二、牛顿法应用举例

三、简化牛顿法与牛顿下山法

四、重根情形

7.4实验课4

生成一个四阶单位矩阵

生成一个三行四列的零矩阵

生成一个三行四列的元素全是1的矩阵

生成一个三行四列的元素全是2的矩阵

生成一个0-1之间均匀分布的随机矩阵

生成一个均值是0，方差是1的标准正态分布随机矩阵

生成对角线元素是已知向量的矩阵

生成行、列、对角线之和都是相同元素的矩阵

提取上下三角矩阵

求逆矩阵

求解线性方程组

线性方程组的系数矩阵：

等式右边的向量：

求解方法：

或者：

求解非线性方程组

二分法求解：

其中“1”表示要求解在1附近的根。

求解刚才的问题（非线性方程组）：

调用函数：

7.5弦截法

1.单点弦截法

2.两点弦截法

3.抛物线法

7.6解非线性方程组的迭代法

7.6实验课

求解非线性方程组：

运行函数的方法：

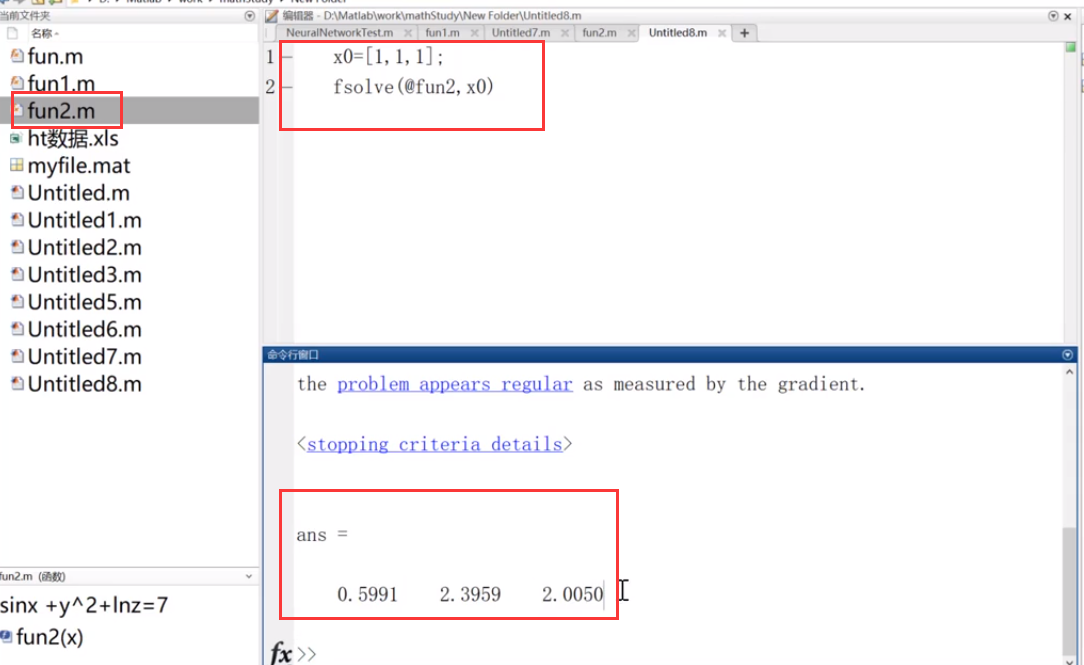
验证方法：

由于结果接近0，因此解成立

练习：

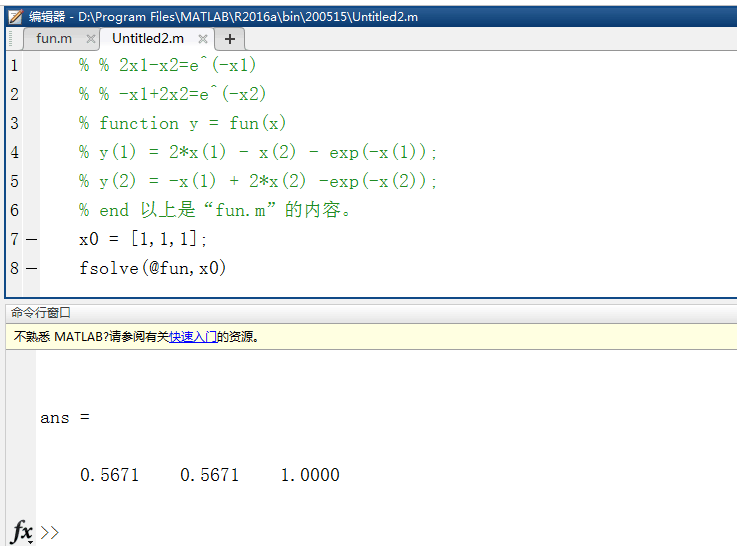
求解非线性方程组：

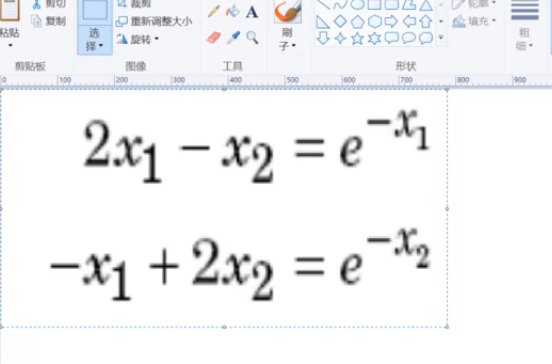
fun.m

% 2x1-x2=e^(-x1)
% -x1+2x2=e^(-x2)
function y = fun(x)
y(1) = 2*x(1) - x(2) - exp(-x(1));
y(2) = -x(1) + 2*x(2) -exp(-x(2));
end

Untitled2.m

x0 = [1,1,1];
fsolve(@fun,x0)

运行结果：

第9章常微分方程初值问题数值解法

9.1引言

科学技术中很多问题都是用常微分方程的定解问题来描述，主要是初值问题和边值问题两大类，本章只考虑初值问题。

很多物理系统与时间相关，从卫星运行轨道到单摆运动，从化学反应到物种竞争都是随时间变化的。

常微分方程式描述连续变化的数学语言。

9.2简单的数值方法与基本概念

1、Euler方法

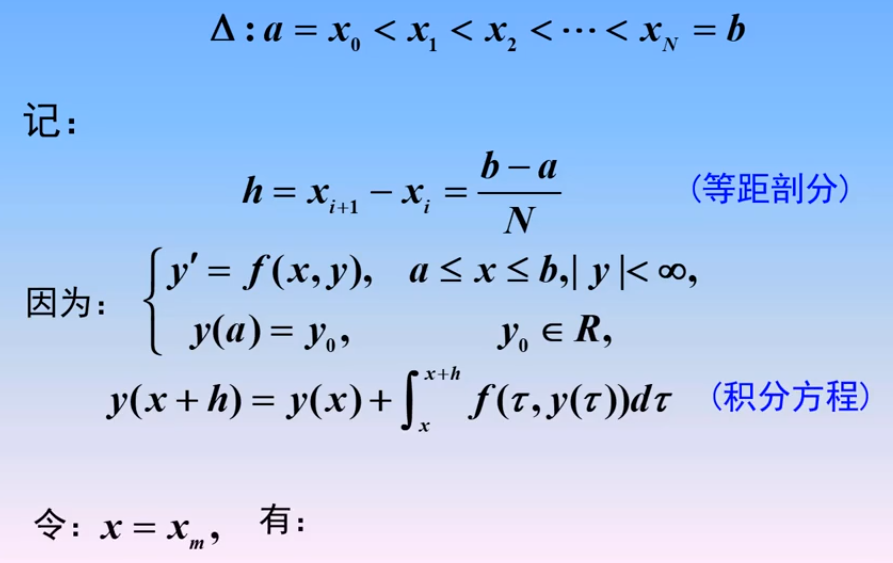
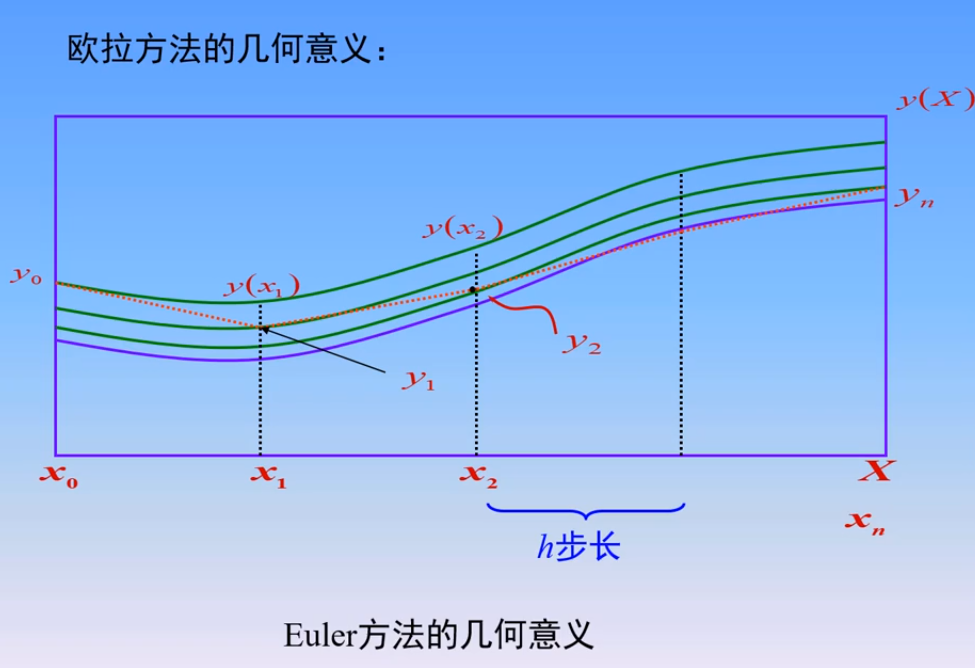
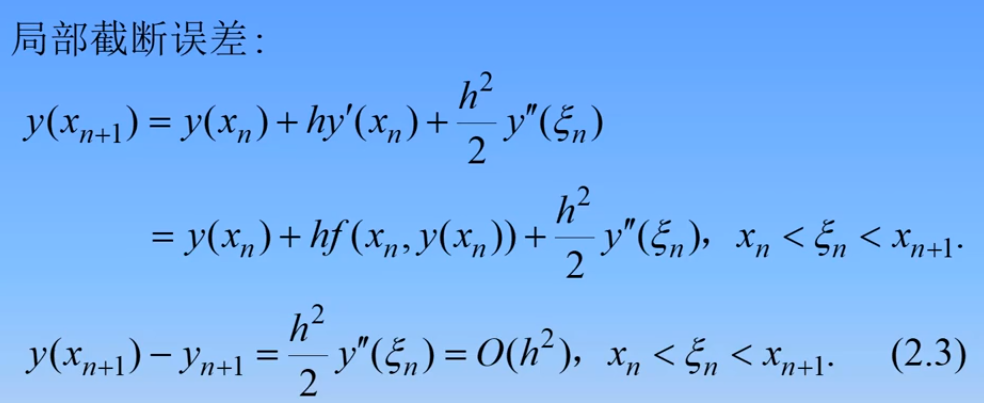
2.梯形方法

3.改进的欧拉公式（预测一校正法）

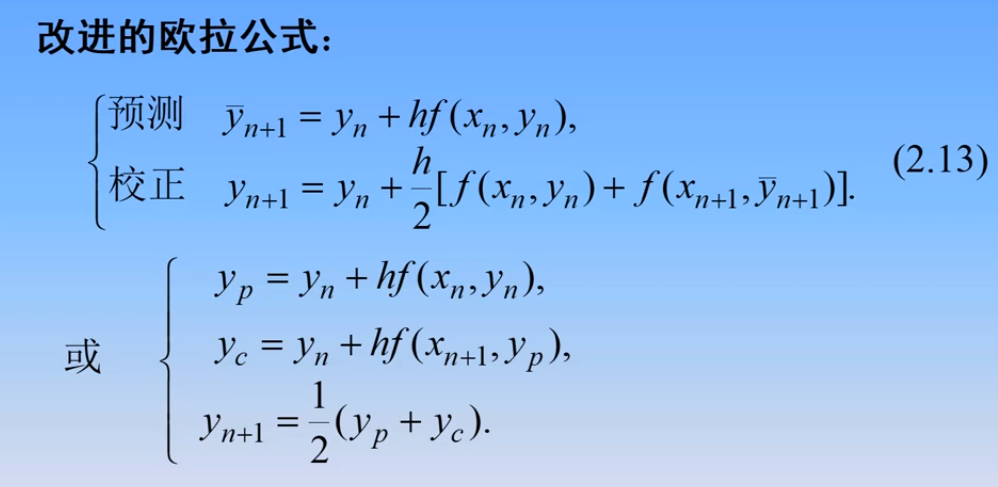
实验课6

用Matlab计算常微分方程：

能解析出解析解的（能用初等函数表达的）：

4.单步法的局部截断误差与阶

9.3龙格一库塔（Runge-Kutta）法

1.显式龙格—库塔法的一般形式

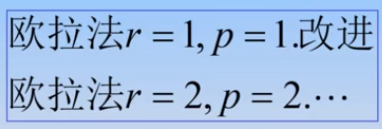
2.二阶显式龙格—库塔方法

3.三阶与四阶显式R-K方法

模拟考试题一：

佬温解答：

版权属于：soarli

本文链接：https://blog.soarli.top/archives/141.html

转载时须注明出处及本声明。